跳到主要内容

信息的表示和处理

信息存储​

基本术语​

字节​
  • 8 bit 的块；
  • 最小的可寻址的内存单位；
地址​
  • 字节在内存中的唯一数字表示；
虚拟地址空间​
  • 地址的集合；

十六进制表示法​

十六进制​

十六进制

二进制和十六进制的转换​
  • 二进制每 4 位分为一组；
  • 总数不是 4 的倍数，最左边一组补 0；
  • 每 4 位 一组转换为对应十六进制；
十进制和十六进制的转换​
  • 整数部分：十进制 x 整数部分整除 16，余数倒序排列；
  • 小数部分；
    • 十进制 x 小数部分乘以 16，记录整数部分；
    • 截取小数部分重复上一步操作，直至乘积小数部分均为 0；
    • 顺序排列整数部分；

二进制表示法​

  • 同十六进制；

字数据大小 (字长)​

  • 决定虚拟地址空间的最大大小；
    • 32 位：4GB；
    • 64 位：16EB；

字节顺序​

  • 小端：低位排在前面；
  • 大端：高位排在前面；

字符串​

  • ASCII 编码 (英文字符，8 位)；
  • Unicode 编码 (32 位)；
  • 不同操作系统具有相同的结果，兼容性好；

代码​

  • 二进制编码；
  • 不同操作系统结果不同；

布尔代数​

  • 与/或/非/异或；

布尔代数

整数表示​

整数数据类型​

  • 32 位 / 64 位；
  • 无符号 / 有符号；

无符号数编码​

  • 设向量 [xw−1,⋯ ,x0][x_{w-1},\cdots,x_0]；
  • 取值范围为 [0,2w−1][0,2^w-1]；

B2Uw(x)=∑i=0w−1xi2iB2U_w(x)=\sum_{i=0}^{w-1}x_i2^i

有符号数​

补码​

计算公式​
  • 设向量 [xw−1,⋯ ,x0][x_{w-1},\cdots,x_0]；
  • 取值范围为 [−2w−1,2w−1−1][-2^{w-1},2^{w-1}-1]；

B2Tw(x)=−xw−12w−1+∑i=0w−2xi2iB2T_w(x)= -x_{w-1}2^{w-1}+ \sum_{i=0}^{w-2}x_i2^i

最值​
  • 由于 0 表示为非负数；
  • |TMin| = |TMax| + 1
重要数字​

重要数字

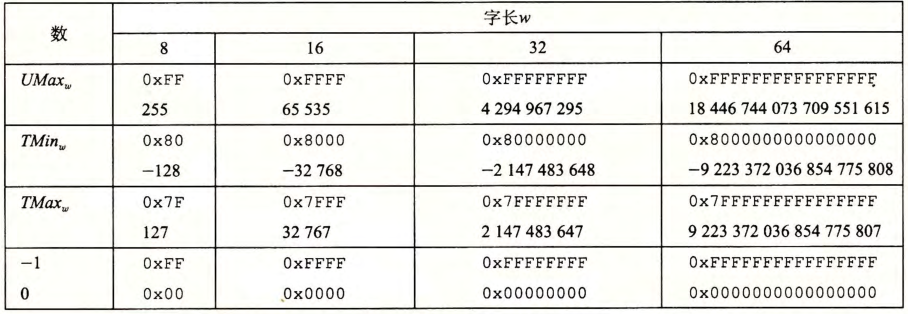
原码和反码​

原码​
  • 最高位表示符号位；
  • 其余位当作无符号数表示；
反码​
  • 最高位权为 −xw−1(2w−1−1)-x_{w-1}(2^{w-1}-1)；
  • 其余同补码；
原码和反码的缺点​
  • -0 和 +0 的编码不同；

从原码到反码/补码​

反码​
  • 原码按位取反；
补码​
  • 反码最低位 +1；

有符号数和无符号数的转换​

原理​
  • 位模式不变，改变位模式的解释方式；
无符号数和补码的转换​

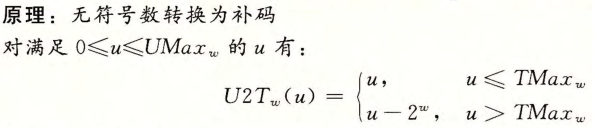
无符号数和补码的转换 无符号数和补码的转换

无符号数和有符号数的拓展​

无符号数拓展 (零拓展)​
  • 无符号数转换为一个更大的数据类型；
  • 只需要在位开头添加 0；
补码拓展 (符号拓展)​
  • 补码表示的有符号数转换为一个更大的数据类型；
  • 只需要在位开头添加符号位；

截断数字​

截断无符号数​
  • 截断高位，保留低位 k 位；
  • x′=xmod2kx'= x mod 2^k；
截断补码数值​
  • 截断高位，保留低位 k 位；
  • x′=U2T(xmod2k)x'= U2T(x mod 2^k)；

整数运算​

无符号加法​

加法​

加法

求反​

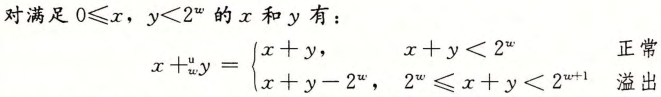
求反

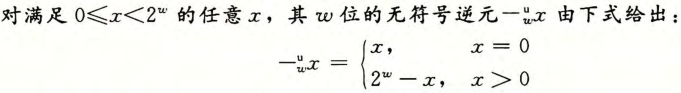
补码加法​

加法​

加法

求反​

求反

无符号乘法​

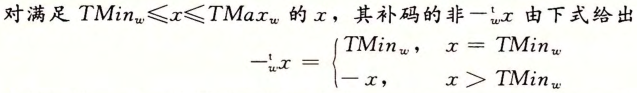
无符号乘法

补码乘法​

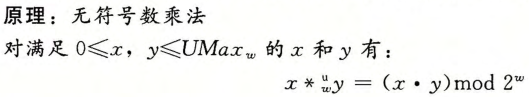
补码乘法

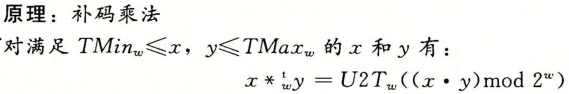
乘以常数​

乘以 2 的幂​
  • 进行左移操作；
  • 位模式右端补 0；
乘以常数​
  • 整数乘法耗费大；
  • 编译器试图通过加减和移位的组合实现整数乘法；

除以 2 的幂​

  • 进行右移操作；
  • 保留位模式左端；
  • x′=⌊x/2k⌋x'= \lfloor x / 2^k \rfloor；

浮点数​

二进制小数​

  • 二进制小数 bm⋯b0.b−1⋯b−nb_m \cdots b_0.b_{-1} \cdots b_{-n}；
  • 其十进制数值为 b=∑i=−nm2i×bIb = \sum^m_{i=-n}2^i \times b_I

IEEE 浮点表示​

IEEE 浮点标准​
  • 使用 V=(−1)s×M×2EV = (-1)^s \times M \times 2^E 的形式近似表示数字；
  • 符号位 s；
  • 尾数 M：一个二进制小数；
  • 阶码 E：对浮点数进行加权；
32 位和 64 位​
  • 32 位：1 + 8 + 23；
  • 64 为：1 + 11 + 52；

32 位和 64 位

规格化的浮点数​
  • 阶码不能全为 1 或 0；
  • 尾数的小数点在最高位有效数字的左边，即 1.xxxx 的形式；

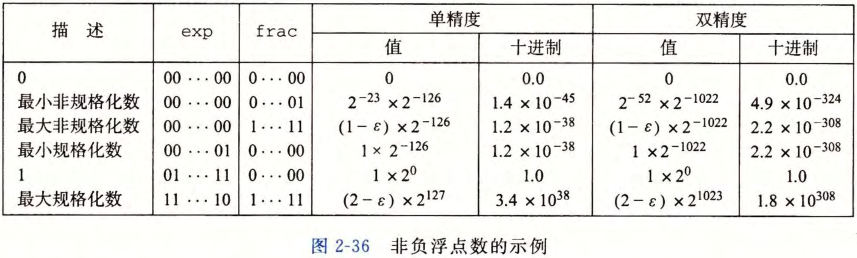
规格化的浮点数的最值

十进制浮点数和 IEEE 的转换​

偏执量​
  • 阶码具有 n 位；
  • 其偏执量为 2^(n-1) - 1；
转换方法​
  • 十进制浮点数转换为二进制小数；
  • 二进制小数转换为规格化的浮点数，即 1.xxx * 2^n 的形式；
  • 取 xxx 并向后补 0 构造尾数；
  • n + 偏执量构造阶码；
  • 添加符号位；
例: 用IEEE754标准将176.0625转换为单精度浮点数
将 176.0625 转换为二进制小数为 10110000.0001
规格化处理: 10110000.0001=1.01100000001 × 2^7, 取小数部分扩展为23位尾数为
01100000001000000000000
阶码为7, 加上偏移量 +127 为 134, 用二进制小数表示为 10000110
符号位为 0
最终单精度浮点数为 01000011001100000001000000000000

舍入​

  • 浮点数只能近似表示数值；
  • 找到最接近的匹配值；

浮点运算​

机制​
  • ⊙\odot 表示任一运算；
  • 浮点运算结果是计算后的舍入结果，是不精确的结果；

x⊙y=Round(x⊙y)x \odot y = Round(x \odot y)