图
图
基础
图
- 一组顶点 V 和一组边 E 的集合;
常见类型
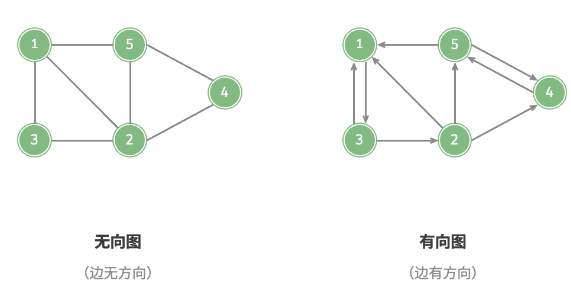
有向图和无向图
- 根据边是否具有方向判定;
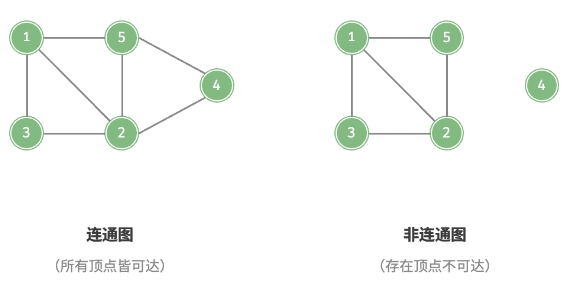
连通图和非连通图
- 从任一顶点出发,可以到达任一顶点,称作连通图;
- 反之称作非连通图;
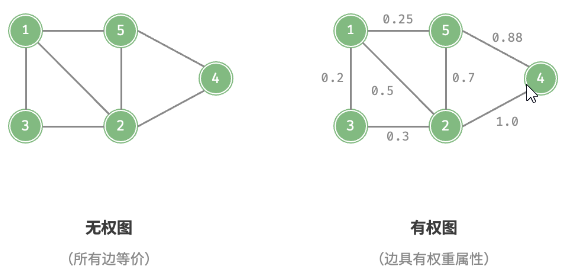
无权图和有权图
- 根据边是否具有权重判定;
常用术语
邻接
- 两顶点存在边相连;
路径
- 从任一顶点到其余任一顶点经过的边构成的序列;
度
- 一个顶点具有的边数;
- 入度:多少条边指向该顶点;
- 出度:多少条边从该顶点指出;
图的表示
邻接矩阵
邻接矩阵
- 若图顶点数量为 n;
- 使用 n*n 的矩阵表示图;
- 通过 0 或 1 表示两顶点是否存在边;
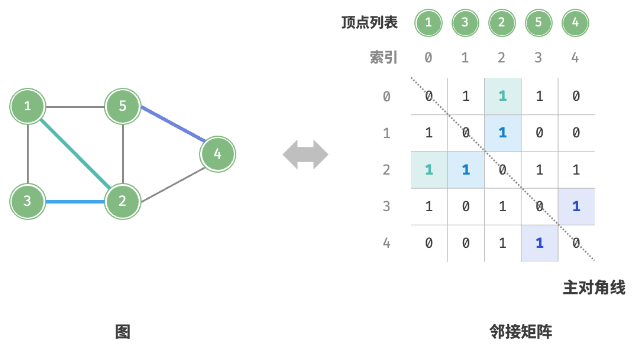
特性
- 邻接矩阵主对角线无意义,恒为 0;
- 无向图关于主对角线对称;
空间复杂度
- O(n^2);
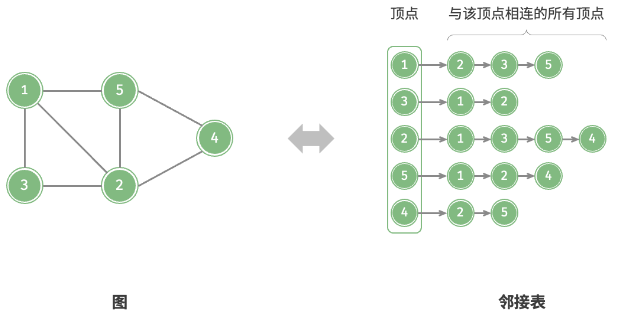
邻接表
邻接表
- 使用 n 个链表表示图;
- 链表节点表示顶点;
- 链表存储顶点的所有邻接顶点;
空间复杂度
- 远小于 O(n^2);
哈希表优化
- 链表使用哈希表;
- n 个哈希表使用哈希表存储;
图的基本操作
基于邻接矩阵
添加和删除边
- 修改矩阵对应元素即可;
添加顶点
- 邻接矩阵尾部添加一行一列;
删除顶点
- 邻接矩阵删除一行一列;
代码
export class GraphAdjMat {
_adjMat: number[][];
_size: number;
_isDirection: boolean;
_index: {
[propName: number]: string;
};
_vertices: {
[propName: string]: number;
};
constructor(vertices: string[], edges: [string, string][]) {
this._vertices = {};
this._adjMat = [];
this._size = 0;
this._isDirection = false;
this._index = {};
for (let index = 0; index < vertices.length; index++) {
const vertex = vertices[index];
this.addVertex(vertex);
}
for (let index = 0; index < edges.length; index++) {
const edge = edges[index];
this.addEdge(edge[0], edge[1]);
}
}
size() {
return this._size;
}
getVertexIndex(value: string) {
const index = this._vertices[value];
if (typeof index === "number") {
return index;
} else {
return null;
}
}
addVertex(value: string) {
const size = this._size;
const newRow = new Array(size).fill(0);
this._vertices[value] = size;
this._index[size] = value;
this._adjMat.push(newRow);
for (let index = 0; index < this._adjMat.length; index++) {
const row = this._adjMat[index];
row.push(0);
}
this._size += 1;
}
removeVertex(value: string) {
const vertexIndex = this.getVertexIndex(value);
if (!(typeof vertexIndex === "number")) {
throw new Error("the graph don't have this vertex");
}
delete this._vertices[value];
delete this._index[vertexIndex];
this._adjMat.splice(vertexIndex, 1);
for (let index = 0; index < this._adjMat.length; index++) {
const row = this._adjMat[index];
row.splice(vertexIndex, 1);
}
this._size -= 1;
}
addEdge(startVertex: string, endVertex: string) {
const startVertexIndex = this.getVertexIndex(startVertex);
const endVertexIndex = this.getVertexIndex(endVertex);
if (
!(
typeof startVertexIndex === "number" &&
typeof endVertexIndex === "number"
)
) {
throw new Error("the graph don't have this vertex");
}
this._adjMat[startVertexIndex][endVertexIndex] = 1;
if (!this._isDirection) {
this._adjMat[endVertexIndex][startVertexIndex] = 1;
}
}
removeEdge(startVertex: string, endVertex: string) {
const startVertexIndex = this.getVertexIndex(startVertex);
const endVertexIndex = this.getVertexIndex(endVertex);
if (
!(
typeof startVertexIndex === "number" &&
typeof endVertexIndex === "number"
)
) {
throw new Error("the graph don't have this vertex");
}
this._adjMat[startVertexIndex][endVertexIndex] = 0;
if (!this._isDirection) {
this._adjMat[endVertexIndex][startVertexIndex] = 0;
}
}
}
基于邻接表
添加边
- 顶点对应链表末尾添加指定顶点;
删除边
- 顶点对应链表删除指定顶点;
添加顶点
- 添加一个链表并作为链表第一个节点;
删除顶点
- 遍历链表,删除指定顶点;
代码实现
import { DoublyLinkedList } from "../linked_list/doubly_linked_list";
import { DoublyLinkedListNode } from "../linked_list/doubly_linked_list_node";
export class GraphVertex {
_value: string;
constructor(value: string) {
this._value = value;
}
get value() {
return this._value;
}
set value(value: string) {
this._value = value;
}
}
export class GraphLinkedList {
_linkList: DoublyLinkedList<GraphVertex>[];
_size: number;
_isDirection: boolean;
constructor(vertices: GraphVertex[], edges: [GraphVertex, GraphVertex][]) {
this._linkList = [];
this._size = 0;
this._isDirection = false;
for (let index = 0; index < vertices.length; index++) {
const vertex = vertices[index];
this.addVertex(vertex);
}
for (let index = 0; index < edges.length; index++) {
const edge = edges[index];
this.addEdge(edge[0], edge[1]);
}
}
size() {
return this._size;
}
getVertexIndex(vertex: GraphVertex) {
for (let index = 0; index < this._size; index++) {
const linkedList = this._linkList[index];
if (vertex === linkedList.head.next?.value) return index;
}
return null;
}
addVertex(vertex: GraphVertex) {
const newLinkedList = new DoublyLinkedList<GraphVertex>();
const node = new DoublyLinkedListNode(vertex);
newLinkedList.insert(node, newLinkedList.head);
this._linkList.push(newLinkedList);
this._size += 1;
}
removeVertex(vertex: GraphVertex) {
const vertexIndex = this.getVertexIndex(vertex);
if (!(typeof vertexIndex === "number")) {
throw new Error("the graph don't have this vertex");
}
this._linkList.splice(vertexIndex, 1);
for (let index = 0; index < this._size - 1; index++) {
const linkedList = this._linkList[index];
const node = linkedList.find(vertex);
if (node) {
linkedList.delete(node);
}
}
this._size -= 1;
}
addEdge(startVertex: GraphVertex, endVertex: GraphVertex) {
const startVertexIndex = this.getVertexIndex(startVertex);
const endVertexIndex = this.getVertexIndex(endVertex);
if (
!(
typeof startVertexIndex === "number" &&
typeof endVertexIndex === "number"
)
) {
throw new Error("the graph don't have this vertex");
}
const linkedList = this._linkList[startVertexIndex];
const node = new DoublyLinkedListNode(endVertex);
linkedList.insert(
node,
linkedList.head.next as DoublyLinkedListNode<GraphVertex>
);
if (!this._isDirection) {
const linkedList = this._linkList[endVertexIndex];
const node = new DoublyLinkedListNode(startVertex);
linkedList.insert(
node,
linkedList.head.next as DoublyLinkedListNode<GraphVertex>
);
}
}
removeEdge(startVertex: GraphVertex, endVertex: GraphVertex) {
const startVertexIndex = this.getVertexIndex(startVertex);
const endVertexIndex = this.getVertexIndex(endVertex);
if (
!(
typeof startVertexIndex === "number" &&
typeof endVertexIndex === "number"
)
) {
throw new Error("the graph don't have this vertex");
}
const linkedList = this._linkList[startVertexIndex];
const node = linkedList.find(endVertex);
if (node) linkedList.delete(node);
if (!this._isDirection) {
const linkedList = this._linkList[endVertexIndex];
const node = linkedList.find(startVertex);
if (node) linkedList.delete(node);
}
}
}
效率对比
效率对比
- n 个顶点和 m 条边;
| 邻接矩阵 | 邻接表 (链表) | 邻接表 (哈希表) | |
|---|---|---|---|
| 判断是否邻接 | |||
| 添加边 | |||
| 删除边 | |||
| 添加顶点 | |||
| 删除顶点 | |||
| 内存空间占用 |
图的遍历(基于邻接表(哈希表))
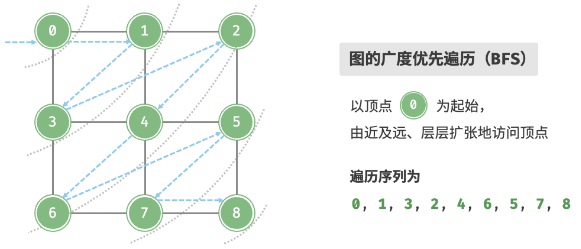
广度优先遍历
思想
- 从一个顶点出发;
- 首先遍历该顶点的所有邻接顶点;
- 然后遍历下一顶点的所有邻接顶点;
- 直至所有顶点遍历完毕;
算法实现
- 使用队列实现,并使用一个哈希表记录顶点是否已经加入队列;
- 起始顶点加入队列并开始迭代;
- 每次迭代弹出队首并记录访问,然后将该顶点的所有邻接顶点加入队尾;
- 循环上一步,直至所有顶点访问完毕;
复杂度
- 时间复杂度:O(V + E);
- 空间复杂度:O(V);
const graph = {
0: ["1", "2"],
1: ["0", "2", "3"],
2: ["0", "1", "3", "4"],
3: ["1", "2", "4", "5"],
4: ["2", "3"],
5: ["3", "6"],
6: [],
};
const bfs = (node) => {
const visited = new Set([node]);
const res = [node];
const queue = [node];
while (queue.length !== 0) {
const curNode = queue.shift();
for (const node of graph[curNode]) {
if (!visited.has(node)) {
res.push(node);
visited.add(node);
queue.push(node);
}
}
}
return res;
};
bfs("0"); // 0 1 2 3 4 5 6
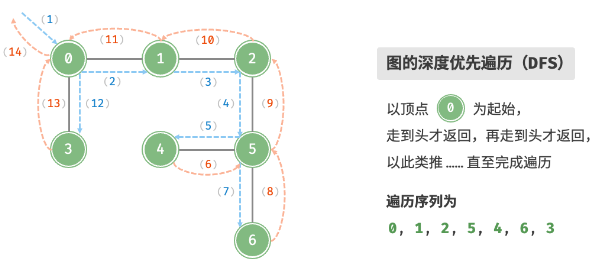
深度优先遍历
思想
- 从一个顶点出发;
- 首先遍历该顶点的某个邻接顶点,走到尽头再返回;
- 依次类推,直至所有顶点遍历完毕;
算法实现
- 使用一个哈希表记录顶点是否已经被访问;
const graph = {
A: ["B", "C"],
B: ["A", "C", "D"],
C: ["A", "B", "D", "E"],
D: ["B", "C", "E", "F"],
E: ["C", "D"],
F: ["D", "G"],
G: [],
};
// 递归实现
const dfs = (node) => {
const res = [node];
const visited = new Set([node]);
const loop = (node) => {
for (const tempNode of graph[node]) {
if (!visited.has(tempNode)) {
visited.add(tempNode);
res.push(tempNode);
loop(tempNode);
}
}
};
loop(node);
return res;
};
// stack 实现
const dfs = (node) => {
const res = [node];
const visited = new Set([node]);
const stack = [node];
while (stack.length !== 0) {
const curNode = stack.pop();
for (const node of graph[curNode]) {
if (!visited.has(node)) {
res.push(node);
visited.add(node);
stack.push(node);
}
}
}
return res;
};
dfs("A"); // A B C D E F G
复杂度
- 时间复杂度:O(V + E);
- 空间复杂度:O(V);
岛屿问题 dfs 模板代码
const dfs = (grid, i, j) => {
const rows = grid.length;
const cols = grid[0].length;
if (i < 0 || i >= rows || j < 0 || j >= cols || grid[i][j] !== "1") {
return 0;
}
grid[i][j] = "2";
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
};
图的遍历题目
岛屿数量
题目
- 200;
思路
- 即求解有多少个连通块;
- 遍历 gird;
- 对于每一个字符为 1 的元素,遍历其上下左右,并赋值为 2;
- 超出边界或字符为 0,返回;
- 每遍历一次,count++;
/**
* @param {character[][]} grid
* @return {number}
*/
var numIslands = function (grid) {
const dfs = (grid, i, j) => {
const rows = grid.length;
const cols = grid[0].length;
if (i < 0 || i >= rows || j < 0 || j >= cols || grid[i][j] !== "1") {
return 0;
}
grid[i][j] = "2";
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
};
let count = 0;
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[0].length; j++) {
if (grid[i][j] === "1") {
dfs(grid, i, j);
count++;
}
}
}
return count;
};
复杂度
- 时间:m * n;
- 空间:m * n;
岛屿的最大面积
题目
- 695;
思路
- 深度优先遍历岛屿;
- 每次遍历中,每搜索一次 1,该岛屿面积 +1;
- 遍历结束,维护最大岛屿面积;
/**
* @param {number[][]} grid
* @return {number}
*/
var maxAreaOfIsland = function (grid) {
const dfs = (grid, i, j) => {
const rows = grid.length;
const cols = grid[0].length;
if (i < 0 || i >= rows || j < 0 || j >= cols || grid[i][j] !== 1) {
return 0;
}
grid[i][j] = 2;
const tem0 = dfs(grid, i, j + 1);
const tem1 = dfs(grid, i, j - 1);
const tem2 = dfs(grid, i + 1, j);
const tem3 = dfs(grid, i - 1, j);
return 1 + tem0 + tem1 + tem2 + tem3;
};
let res = 0;
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[0].length; j++) {
if (grid[i][j] === 1) {
const area = dfs(grid, i, j);
res = Math.max(area, res);
}
}
}
return res;
};
复杂度
- 时间:m * n;
- 空间:m * n;
求根节点到叶节点数字子和
题目
- 129;
思路
- 基于深度优先遍历;
- 记录路径构成数字;
- 遇到叶节点,返回当前叶节点值;
- 反之遍历左右子树,累加结果;
- 基于回溯;
- 记录路径数字;
- 到达叶节点,路径转换为数字,累加至结果;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var sumNumbers = function (root) {
const dfs = (node, sum) => {
if (node == null) return 0;
sum = node.val + 10 * sum;
if (node.left == null && node.right == null) return sum;
const left = dfs(node.left, sum);
const right = dfs(node.right, sum);
return left + right;
};
const res = dfs(root, 0);
return res;
};
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var sumNumbers = function (root) {
const backtrack = (res, state, node) => {
if (node.left == null && node.right == null) {
res.push(Number(state.join("")));
return;
}
if (node.left != null) {
state.push(node.left.val);
backtrack(res, state, node.left);
state.pop();
}
if (node.right != null) {
state.push(node.right.val);
backtrack(res, state, node.right);
state.pop();
}
};
const res = [];
if (root == null) return 0;
backtrack(res, [root.val], root);
return res.reduce((a, b) => a + b, 0);
};
复杂度
- 时间:n;
- 空间:n;
二叉树的直径
题目
- 543;
思路
- 树中两个节点之间的最大距离;
- 经过根节点:左子树高度 + 右子树高度;
- 不经过根节点:子树的最大路径长度;
- 二叉树直径 = max(所有子树的最大路径,左子树高度 + 右子树高度);
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var diameterOfBinaryTree = function (root) {
let res = -1;
const dfs = (node) => {
if (node == null) return 0;
const left = dfs(node.left);
const right = dfs(node.right);
res = Math.max(res, right + left);
return Math.max(left, right) + 1;
};
dfs(root);
return res;
};
复杂度
- 时间:n;
- 空间:n;
二叉树最大宽度
题目
- 662;
思路
- 基于广度优先遍历;
- 对于 level,同时记录节点索引;
- level 构建完毕,计算索引差值,维护最大宽度;
- 此题会超出 js 最大 Int,使用 BigInt;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var widthOfBinaryTree = function (root) {
const queue = [[root, 0n]];
let res = 0n;
while (queue.length !== 0) {
const size = queue.length;
const width = queue[size - 1][1] - queue[0][1] + 1n;
if (width > res) res = width;
for (let i = 0; i < size; i++) {
const [node, index] = queue.shift();
if (node.left != null) queue.push([node.left, 2n * index + 1n]);
if (node.right != null) queue.push([node.right, 2n * index + 2n]);
}
}
return res;
};
复杂度
- 时间:n;
- 空间:n;
拓扑排序
应用场景
- 验证有向无环图是否存在环路;
基本思想
- 基于队列优先遍历;
- 不断删除入度为 0 的节点;
算法步骤
- 初始化一个栈;
- 添加所有入度为 0 的节点至栈;
- 循环执行以下步骤直至栈为空;
- 栈中取出一个节点,添加至结果队列;
- 遍历该节点的所有邻接节点,将邻接节点入度 -1;
- 若邻接节点的入度变为 0,添加至栈;
- 若结果队列中包含图中的所有节点,则 DAO 中不存在环,反之存在环;
const graph = {
1: ["2", "3"],
2: ["3", "4"],
3: ["4", "5"],
4: ["5", "6"],
5: [],
6: [],
};
const topologicalSort = (graph) => {
const inDegree = {};
for (const node of Object.keys(graph)) {
inDegree[node] = 0;
}
for (const neighbors of Object.values(graph)) {
for (const neighbor of neighbors) {
inDegree[neighbor]++;
}
}
const res = [];
const stack = [];
for (const [node, degree] of Object.entries(inDegree)) {
if (degree === 0) {
stack.push(node);
res.push(node);
}
}
while (stack.length !== 0) {
const curNode = stack.pop();
for (const neighbor of graph[curNode]) {
inDegree[neighbor]--;
if (inDegree[neighbor] === 0) {
res.push(neighbor);
stack.push(neighbor);
}
}
}
return res.length === Object.keys(graph).length ? [true, res] : [false, null];
};
topologicalSort(graph); // true
拓扑排序题目
课程表 1
题目
- 207;
思路
- 根据课程关系构建图;
- 使用拓扑排序,判断结果数量和课程数量;
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @return {boolean}
*/
var canFinish = function (numCourses, prerequisites) {
const topology = (graph, numCourses) => {
const inDegree = {};
for (const node of Object.keys(graph)) {
inDegree[node] = 0;
}
for (const node of Object.keys(graph)) {
for (const neighbor of graph[node]) {
if (inDegree[neighbor] != null) inDegree[neighbor]++;
}
}
const stack = [];
const res = [];
for (const [node, degree] of Object.entries(inDegree)) {
if (degree !== 0) continue;
stack.push(node);
res.push(node);
}
while (stack.length !== 0) {
const node = stack.pop();
for (const neighbor of graph[node]) {
inDegree[neighbor]--;
if (inDegree[neighbor] === 0) {
stack.push(neighbor);
res.push(neighbor);
}
}
}
return res.length === numCourses;
};
const graph = {};
for (let i = 0; i < numCourses; i++) {
graph[i] = [];
}
for (const [a, b] of prerequisites) {
if (graph[b] != null) graph[b].push(a);
}
return topology(graph, numCourses);
};
复杂度
- 时间:m + n;
- 空间:m + n;
课程表 2
题目
- 210;
思路
- 根据课程关系构建图;
- 使用拓扑排序,返回结果即可;
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @return {number[]}
*/
var findOrder = function (numCourses, prerequisites) {
const topology = (graph) => {
const inDegree = {};
for (const node of Object.keys(graph)) {
inDegree[node] = 0;
}
for (const node of Object.keys(graph)) {
for (const neighbor of graph[node]) {
if (inDegree[neighbor] != null) inDegree[neighbor]++;
}
}
const stack = [];
const res = [];
for (const [node, degree] of Object.entries(inDegree)) {
if (degree !== 0) continue;
stack.push(node);
res.push(node);
}
while (stack.length !== 0) {
const node = stack.pop();
for (const neighbor of graph[node]) {
inDegree[neighbor]--;
if (inDegree[neighbor] === 0) {
stack.push(neighbor);
res.push(neighbor);
}
}
}
return res.length === Object.keys(graph).length ? res : [];
};
const graph = {};
for (let i = 0; i < numCourses; i++) {
graph[i] = [];
}
for (const [a, b] of prerequisites) {
if (graph[b] != null) graph[b].push(a);
}
return topology(graph, numCourses);
};
复杂度
- 时间:m + n;
- 空间:m + n;