跳到主要内容

绪论

算法​

算法​
  • 特定计算机模型；
  • 解决特定问题的指令序列；
算法的特征​
  • 输入 + 输出；
  • 正确性：可以解决特定问题；
  • 确定性：描述为指令序列；
  • 可行性：可在常数时间内完成；
  • 有穷性：任何输入，经过有穷次操作，都可得到输出；
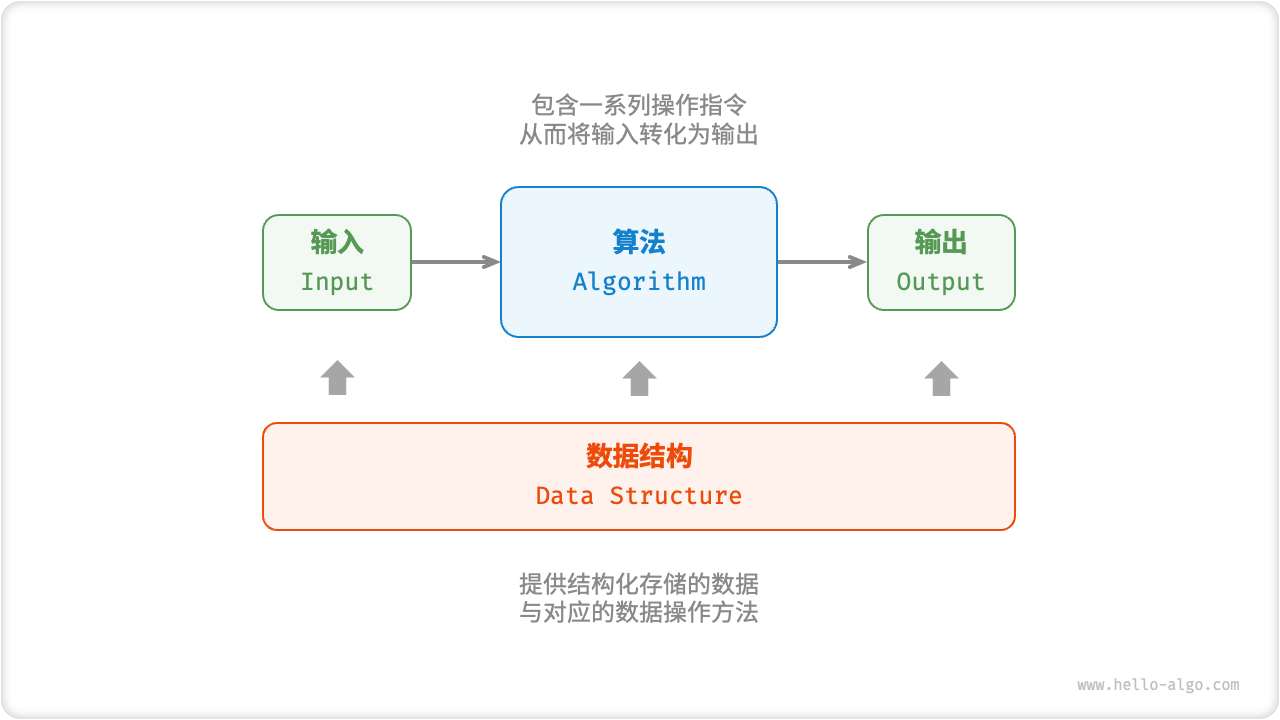
数据结构​
  • 计算机中组织和存储数据的方式；
数据结构和算法的关系​

数据结构和算法的关系

复杂度​

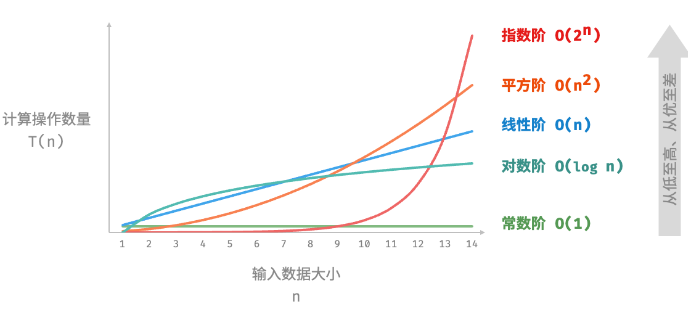
时间复杂度​

时间复杂度​
  • 依次为最差时间复杂度，最佳时间复杂度，平均时间复杂度；

T(n)=O(f(n))if∃c>0s.t.T(n)<c⋅f(n)∀n≫2T(n) = \Omicron(f(n)) \qquad if \exist c>0 \qquad s.t. \quad T(n) < c \cdot f(n) \qquad \forall n \gg 2 T(n)=Ω(f(n))if∃c>0s.t.T(n)>c⋅f(n)∀n≫2T(n) = \Omega(f(n)) \qquad if \exist c>0 \qquad s.t. \quad T(n) > c \cdot f(n) \qquad \forall n \gg 2 T(n)=Θ(f(n))if∃c1>c2>0s.t.c1⋅f(n)>T(n)>c2⋅f(n)∀n≫2T(n) = \Theta(f(n)) \qquad if \exist c_1>c_2>0 \qquad s.t. \quad c_1 \cdot f(n) > T(n) > c_2 \cdot f(n) \qquad \forall n \gg 2

层次划分​

层次划分 层次划分

时间复杂度的计算​
  • for 循环：运行时间 * 迭代次数；
  • 嵌套 for 循环：for 循环的乘积；
  • 顺序语句：时间求和；
  • 条件语句：对应块中的最大运行时间；
常数阶​
function constant(n) {
  let count = 0;
  const size = 100000;
  for (let i = 0; i < size; i++) count++;
  return count;
}
线性阶​
// 常见于单层循环
function linear(n) {
  let count = 0;
  for (let i = 0; i < n; i++) count++;
  return count;
}
平方阶​
// 常见于嵌套循环
function quadratic(n) {
  let count = 0;
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; j++) {
      count++;
    }
  }
  return count;
}
指数阶​
// 常见于循环枚举
function exponential(n) {
  let count = 0,
    base = 1;
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < base; j++) {
      count++;
    }
    base *= 2;
  }
  return count;
}
对数阶​
// 常见于二分查找或分治算法
function logarithmic(n) {
  let count = 0;
  while (n > 1) {
    n = n / 2;
    count++;
  }
  return count;
}
线性对数阶​
// 常见于嵌套循环
function linearLogRecur(n) {
  if (n <= 1) return 1;
  let count = linearLogRecur(n / 2) + linearLogRecur(n / 2);
  for (let i = 0; i < n; i++) {
    count++;
  }
  return count;
}
阶乘阶​
// 常见于递归
function factorialRecur(n) {
  if (n == 0) return 1;
  let count = 0;
  for (let i = 0; i < n; i++) {
    count += factorialRecur(n - 1);
  }
  return count;
}

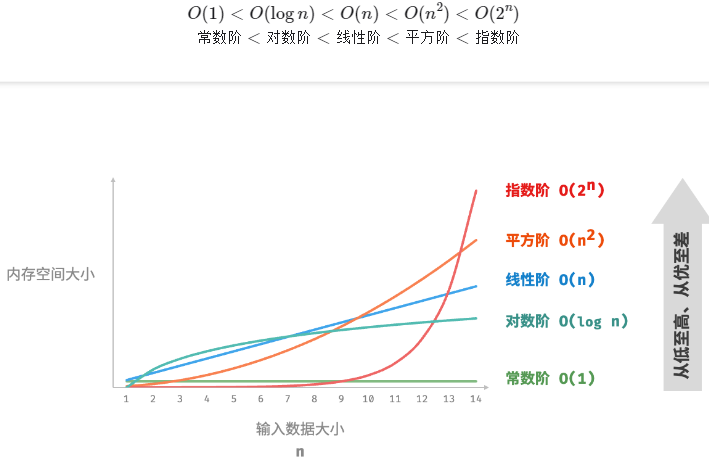
空间复杂度​

相关空间​
  • 输入空间：存储输入数据；
  • 暂存空间：存储运行数据；
  • 输出空间：存储输出数据；
计算方法​
  • 以最差输入数据为准；
  • 以峰值内存为准；
常见类型​

常见类型

常数阶​
// 常见于与输入数据无关的变量, 对象
function constant(n) {
  // 常量, 变量, 对象占用 O(1) 空间
  const a = 0;
  const b = 0;
  const nums = new Array(10000);
  const node = new ListNode(0);
  // 循环中的变量占用 O(1) 空间
  for (let i = 0; i < n; i++) {
    const c = 0;
  }
  // 循环中的函数占用 O(1) 空间
  for (let i = 0; i < n; i++) {
    constFunc();
  }
}
线性阶​
// 常见于与输入数据有关的数组, 表, 栈, 队列等
function linear(n) {
  // 长度为 n 的数组占用 O(n) 空间
  const nums = new Array(n);
  // 长度为 n 的列表占用 O(n) 空间
  const nodes = [];
  for (let i = 0; i < n; i++) {
    nodes.push(new ListNode(i));
  }
  // 长度为 n 的哈希表占用 O(n) 空间
  const map = new Map();
  for (let i = 0; i < n; i++) {
    map.set(i, i.toString());
  }
}
平方阶​
// 常见于矩阵, 图
function quadratic(n) {
  // 矩阵占用 O(n^2) 空间
  const numMatrix = Array(n)
    .fill(null)
    .map(() => Array(n).fill(null));
  // 二维列表占用 O(n^2) 空间
  const numList = [];
  for (let i = 0; i < n; i++) {
    const tmp = [];
    for (let j = 0; j < n; j++) {
      tmp.push(0);
    }
    numList.push(tmp);
  }
}
指数阶​
// 常见于二叉树
function buildTree(n) {
  if (n === 0) return null;
  const root = new TreeNode(0);
  root.left = buildTree(n - 1);
  root.right = buildTree(n - 1);
  return root;
}
对数阶​
  • 常见于分治算法和数据类型转化；

数据结构​

逻辑结构​

线性结构​
  • 数组；
  • 链表；
  • 栈；
  • 队列；
  • 哈希表；
非线性结构​
  • 树形结构；
    • 树；
    • 堆；
    • 哈希表；
  • 网状结构；
    • 图；

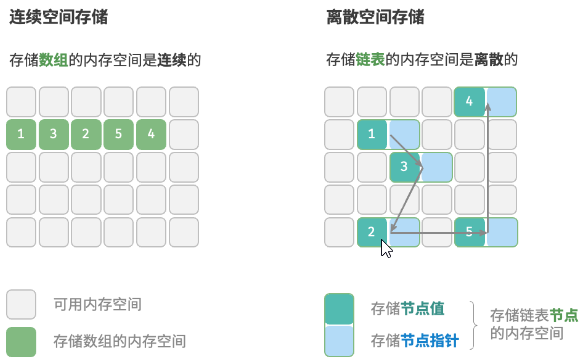
物理结构​

连续空间存储和离散空间存储​
  • 存储数组的内存空间是连续的；
  • 存储链表的内存空间是离散的；

连续空间存储和离散空间存储

可基于数组实现的数据结构​
  • 栈 + 队列 + 哈希表 + 树 + 堆 + 图 + 矩阵；
可基于链表实现的数据结构​
  • 栈 + 队列 + 哈希表 + 树 + 堆；