函数依赖
函数依赖
- 关系 R 上的函数依赖是指若 R 的两个元组在若干属性 A 上属性值相同;
- 那两者必定在若干属性 B 上属性值相同;
- 记作 A1A2⋯An→B1B2⋯Bm;
- 称 A 函数决定 B;
关系的键
- 若下列条件满足,则认为属性集 {A1A2⋯An} 是关系 R 的键;
- 关系 R 不可能存在两个元组在属性集 A 上存在相同的属性值;
最小的键
- 若属性集 A 是关系 R 的键;
- 若属性集 A 的任一真子集都不是 R 的键;
- 则称属性集 A 是最小的键;
传递依赖和直接依赖
- 传递依赖:使用传递规则成立的依赖;
- 直接依赖:非传递依赖;
部分依赖
- 若 A 函数决定 B,存在 A 的真子集函数决定 B;
- 则称 B 部分函数依赖 A;
完全依赖
- 若 A 函数决定 B,任一 A 的真子集都不函数决定 B;
- 则称 B 完全函数依赖 A;
多值依赖 (MVD)
- 对于 R 中每个在 A 上属性一致的元组对 t 和 u,R 中总满足下列条件的元组;
- 在 A 上取值与 t 和 u 相同;
- 在 B 上取值与 t 相同;
- 在不属于 A 和 B 的其他属性上与 u 相同;
函数依赖规则
分解/结合规则
- 左边 FD 等效于右边 FD;
- 分解规则;
- A1A2⋯An→Bi(i=1,2,⋯,m)⇒A1A2⋯An→B1B2⋯Bm
- 结合规则;
- A1A2⋯An→B1B2⋯Bm⇒A1A2⋯An→Bi(i=1,2,⋯,m)
传递规则
- 若 A1A2⋯An→B1B2⋯Bm,B1B2⋯Bm→C1C2⋯Ck;
- 则 A1A2⋯An→C1C2⋯Ck;
Armstrong 公理

关系数据库模式设计
常见异常
- 冗余:属性在多个元组重复;
- 更新异常:修改某一元组属性,但没有修改其他元祖的相同属性;
- 删除异常:一个值集变为空值引起副作用;
函数范式
第一范式 (1NF)
第二范式 (2NF)
- 关系表必须有一个主键;
- 关系表其他列必须完全依赖于主键;
- 消除部分函数依赖;
第三范式 (3NF)
- 若 R 中的任意非平凡 FD A1A2⋯An→B1B2⋯Bm 成立;
- 或属性集 A 是关系 R 的超键,或 B 是关系表键的子集;
- 关系表必须有一个主键;
- 关系表其他列必须直接依赖于主键;
- 消除传递依赖;
BCNF
- 若 R 中的任意非平凡 FD A1A2⋯An→B1B2⋯Bm 成立;
- 则属性集 A 是关系 R 的超键,即任意非平凡函数依赖的左边必须是键;
- BCNF 是修正后,更为严格的 3NF;
第四范式 (4NF)
- 若 R 中的任意非平凡 MVD A1A2⋯An→→B1B2⋯Bm 成立;
- 则属性集 A 是超键,即任一非平凡 MVD 的左边必须是超键;
- 消除多值依赖;
范式的联系
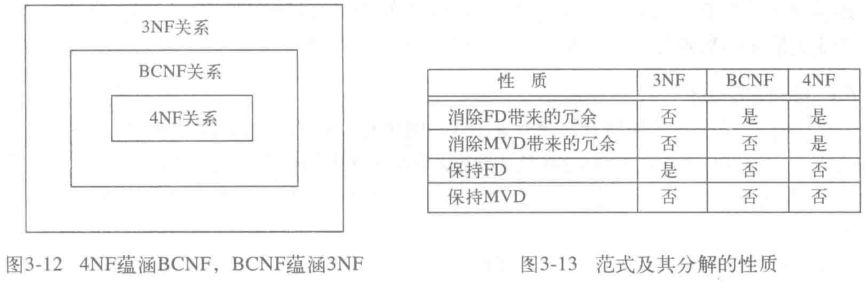
分解方法
BCNF
- 找到违反 BCNF 的非平凡依赖;
- 保留右边的一个属性于原关系表;
- 将其右边建立一个新的关系表;
- 接着对新建立的关系表进行 BCNF 分解;
多值依赖
- 找到违反 MVD 的非平凡依赖;
- 将属性集 A 和 B 建立一个关系表;
- 不属于 A 和 B 的属性建立另一个关系表;
- 接着对新建立的关系表进行 MVD 分解;

