线性代数中的线性方程组

线性方程组

基础

线性方程

$a_1x_1 + a_2x_2 + ... + a_nx_n = b$

线性方程组

• 多个包含相同变量的线性方程；

解和解集

• 线性方程组的解是一组数，使线性方程组成立；
• 所有解的集合称作线性方程组的解集；
• 若两个线性方程组具有相同的解集，则两个线性方程组等价；

解的情况

• 无解；
• 唯一解；
• 无穷多解；

相容和不相容

• 若线性方程组有唯一解或无穷多解；
• 称其为相容，否则不相容；

矩阵记号

线性方程组示例

$\begin{aligned} x_1 - 2x_2 + x_3 = 0 \\ 2x_2 - 8x_3 = 8 \\ 5x1 - 5x_3 = 10 \end{aligned}$

系数矩阵

$\begin{vmatrix} 1 & -2 & 1 \\ 0 & -2 & -8 \\ 5 & 0 & -5 \\ \end{vmatrix}$

增广矩阵

$\begin{vmatrix} 1 & -2 & 1 & 0 \\ 0 & -2 & -8 & 8\\ 5 & 0 & -5 & 10\\ \end{vmatrix}$

维数

• 矩阵的行数和列数；
• $m \times n$ 矩阵为 m 行 n 列；

解线性方程组

基本思路

• 转换成更简单的等价方程组；

初等行变换

• 倍加变换：方程变换为其与另一个方程的倍数的和；
• 对换变换：交换方程位置；
• 倍乘变换：某个方程所有项乘以非零数；

行等价

• 经过初等行变换的矩阵是行等价的；
• 具有相同的解集；

行化简与阶梯型矩阵

基础

先导元素

• 非零行中最左边的非零元素；

行阶矩阵

• 每一非零行都在每一零行之上；
• 某一行的先导元素所在的列位于前一行先导元素的右边；
• 某一先导元素所在列下方元素都是零；

简化行阶矩阵

• 每一非零行的先导元素是 1；
• 每一先导元素 1 是该元素所在列的唯一非零元素；

简化行阶矩阵的唯一性

• 每个矩阵行等价于唯一的简化阶梯形矩阵；

符号表示

• 行阶矩阵：A/REF；
• 化简行阶矩阵：U/RREF；

主元位置

主元位置

• A 中对应于它的行阶矩阵中先导元素 1 的位置；

主元列

• A 含有主元位置的列；

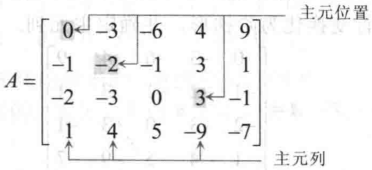
行化简算法

步骤

• 选择最左的非零列 (存在多个选择数值最大的) 放置于顶端并将其作为主元；
• 利用倍加行变换将该主元下面的元素变为 0；
• 选择次左的非零列，递归使用以上步骤；
• 从最右的主元开始，首先利用倍乘变换将其变为 1，在把主元的上方元素变为 0；

线性方程的解

基本变量和自由变量

• 基本变量：位于主元列的变量，如 x1，x2；
• 其他变量：如 x3；

$\begin{vmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & -8 & 8\\ 0 & 0 & 0 & 0\\ \end{vmatrix}$

通解

$\begin{cases} x_1 = 1+5x_3 \\ x_2=4-x_3\\ x3 \text{是自由变量} \\ \end{cases}$

存在和唯一性问题

存在和唯一性定理

• 线性方程组相容的充要条件为增广矩阵的最右列不是主元列；
• 若线性方程组相容；
  • 无自由变量：唯一解；
  • 有自由变量：无穷解；

$[0 \cdots 0 b],\quad b \neq 0$

向量方程

$R^2$ 中的向量

列向量

• 仅有一列的矩阵，简称向量；

$$u=\begin{vmatrix} 3\\ -1 \end{vmatrix}$$

向量相等

• 矩阵对应元素相对能；

向量加法

$$\begin{vmatrix} 3\\ -1 \end{vmatrix} + \begin{vmatrix} 1 \\ 1 \end{vmatrix}= \begin{vmatrix} 3+1\\ -1+1 \end{vmatrix}= \begin{vmatrix} 4\\ 0 \end{vmatrix}$$

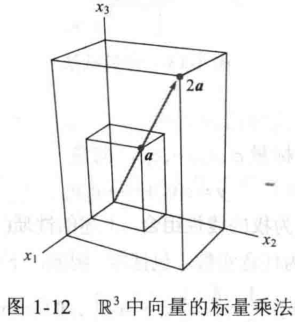
标量乘法

• 若 c 为实数 5 (又称为标量)；
• u 为向量；

$$cu= 5 \begin{vmatrix} 2 \\ 1 \end{vmatrix}= \begin{vmatrix} 10\\ 5 \end{vmatrix}$$

向量的简写

• (3，1)；

$R^2$的几何表示

• (x，y) 的几何表示为 (0，0) 指向 (x，y) 的有向线段；

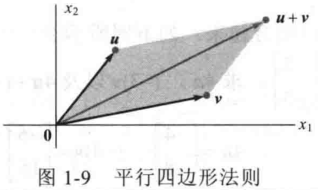
向量加法的平行四边形法则

• u + v 对应以 u，v，原点为第三个顶点构成的平行四边形；

$R^3$ 中的向量

几何表示

• (x，y，z) 的几何表示为 (0，0，0) 指向 (x，y，z) 的有向线段

$R^n$ 中的向量

矩阵形式

$$u= \begin{vmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{vmatrix}$$

零向量

• 所有矩阵元素都是 0 的向量；

向量的代数性质

线性组合

线性组合

• 给定向量 $v_1, ... v_n$；
• 标量 $c_1, ... c_n$；
• 称下述公式为以 $c_1, ... c_n$ 为权的线性组合；

$y=c_1 v_1+\cdots+c_p v_p$

向量方程和增广矩阵

• $x_1 a_1+\cdots+x_n a_n=b$ 和 $[a_1 \cdots a_n \quad b]$ 有相同的解集；

张成

• 若 $v_1, ... v_n$ 是 $R^n$ 的向量；
• 则 $v_1, ... v_n$ 的所有线性组合构成的结合通过 $Span\{v_1, ... v_n\}$ 表示；
• 称作 $v_1, ... v_n$ 张成的 $R^n$ 的子集；

向量方程

• 判断向量 b 是否属于 $Span\{v_1, ... v_n\}$；
• 即判断下列向量方程是否有解；

$c_1 v_1+\cdots+c_p v_p = b$

Span{v} 和 Span{u, v} 的几何表示

Span{v}

• 设 v 是 R3 中的向量；
• Span{v} 是 v 所有标量倍数的集合；
• 即过 v 和 0 的直线上所有点的集合；

Span{u, v}

• 设 u，v 是 R3 中的向量；
• Span{u，v} 是过 u，v 和 0 的平面上所有点的集合；
• Span{u，v} 包括 Span{u} 和 Span{v}

矩阵方程

矩阵方程

Ax=b

• 若 A 为 m 行 n 列的矩阵，各列依次为 a1，。。。，an；
• 若 x 是 $R^n$ 中的向量；
• 则 Ax 为 A 各列以 x1，。。。，xn 为权的线性组合；
• A 的列数和向量个数相同；

$Ax=[a_1,...,a_n] \begin{vmatrix} x_1 \\ \vdots \\ x_n \end{vmatrix} = x_1a_1+\cdots+ x_na_n$

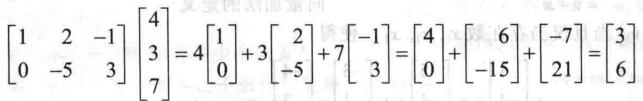
矩阵方程

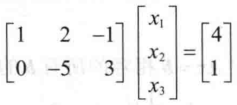
矩阵方程和向量方程和增广矩阵

• 若 A 为 m 行 n 列的矩阵，各列依次为 a1，。。。，an；
• 若 x 是 $R^n$ 中的向量；
• 则 $Ax=b$ 和 $x_1 a_1+\cdots+x_n a_n=b$ 和 $[a_1 \cdots a_n \quad b]$ 有相同的解集；

解的存在性

解的存在性

• 方程 Ax=b 有解当且仅当 b 是 A 各列的线性组合；

mn 矩阵的定理

• mn 矩阵为系数矩阵；

Ax 的向量规则

• 若 Ax 有定义；
• Ax 的第 n 个元素为 A 的第 n 行与 x 对应元素乘积之和；

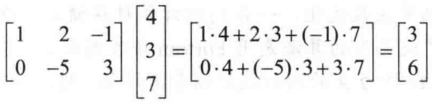
Ax 的性质

线性方程组的解集

齐次线性方程组

齐次线性方程组

• 可以写成 Ax=0 矩阵方程形式的线性方程组称作齐次的；
• 至少有一个解 x = 0 称作平凡解；
• 满足 Ax=0 的非零向量称作非平凡解；
  • 仅当齐次方程存在自由变量时才有非平凡解；

几何意义

• 仅有平凡解：Span{0}；
• 一个非平凡解：过 0 的一条直线；
• 多个非平凡解：过原点的平面。。。

参数向量形式

参数向量方程

• 下列方程称为平面的参数向量方程；
• 同理推广至线，体；

$x=su+tv$

参数向量方程形式的转换

非齐次线性方程组的解

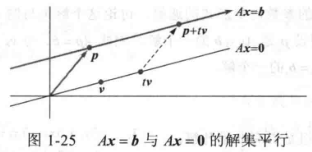
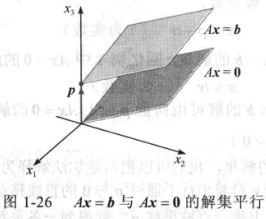
非齐次线性方程组的解

• 若 Ax = b 对于某个 b 是相容的
• p 为其一个特解；
• Ax = b 的解集是 w = p + v 的向量的集合
• v 是 Ax = 0 中的任意解；
• 两者解集平行；

线性无关

基础

线性无关

• 若一组向量 {v1, ..., vp} 称作线性无关；
• 则向量方程 x1v1 + 。。。+ x_pv_p = 0 仅有平凡解；

线性相关

• 若一组向量 {v1, ..., vp} 称作线性相关；
• 则向量方程 x1v1 + 。。。+ x_pv_p = 0 存在非平凡解；

矩阵各列的线性无关

矩阵各列的线性无关

• 矩阵 A 各列线性无关；
• 仅当 Ax = 0 仅有平凡解；

一个或多个个向量的集合

一个向量

• 零向量是线性相关的；
• 其余向量为线性无关；

线性相关集的特征

• 若向量集合 S = {v1, ..., v2} 线性相关；
• 则向量集合至少有一个向量是其他向量的线性组合；

定理

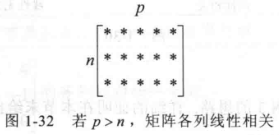
• 若一组向量的向量个数超过每个向量的维度；
• 这个向量组线性相关；

定理

• 若向量组中包含零向量；
• 这个向量组线性相关；

线性变换介绍

基础

变换

• 从 $R^n$ 到 $R^m$ 的一个变换；
• 把 $R^n$ 的各向量 x 对应 $R^m$ 的一个向量 T(x)；
• $R^n$ 称作 T 的定义域；
• $R^m$ 称作 T 的余定义域；
• T(x) 称为 x 的像；
• T(x) 的集合称为 T 的值域；

矩阵变换

简写

• 一个矩阵变换记作 $x \rightarrow Ax$；

线性变换

线性变换

• 满足下列条件的变化称作线性变换；
  • 对于 T 的定义中的任何 u，v，T(u + v) = T(u) + T(v)；
  • 对于 T 的定义中的任何 u 和常量 c，T(cu) = cT(u)；
• 每个矩阵都是线性变换；

线性变换的性质

• T(0) = 0；
• T(c1v1 + 。。。+ cpvp) = c1T(v1) + 。。。+ cpT(vp)

线性变换的矩阵

线性变换的标准矩阵

常见的几何线性变换

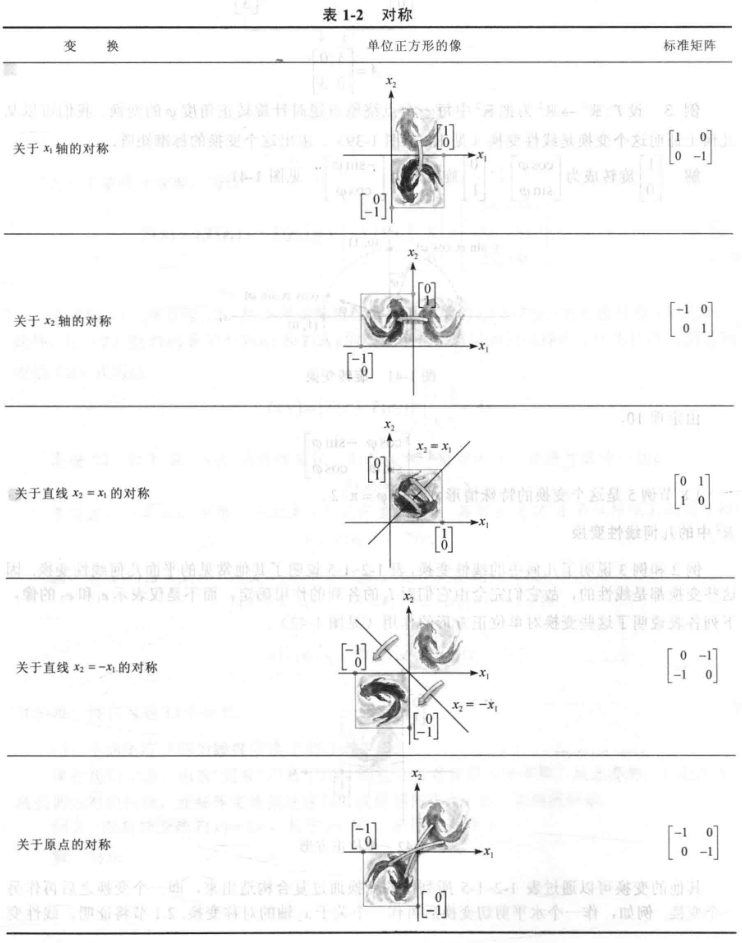
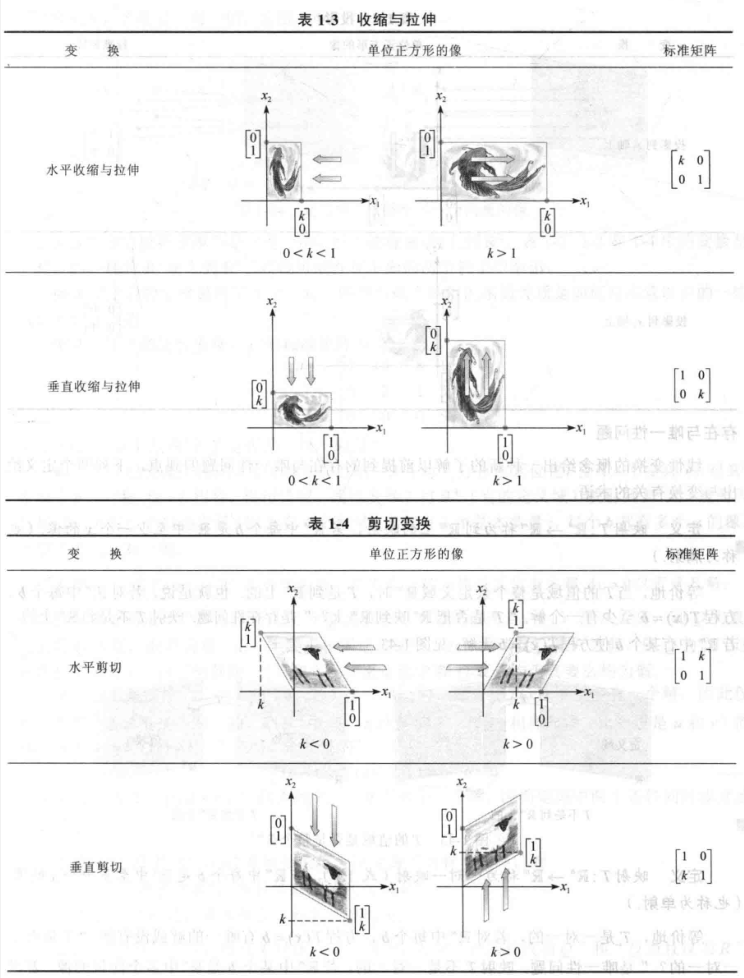
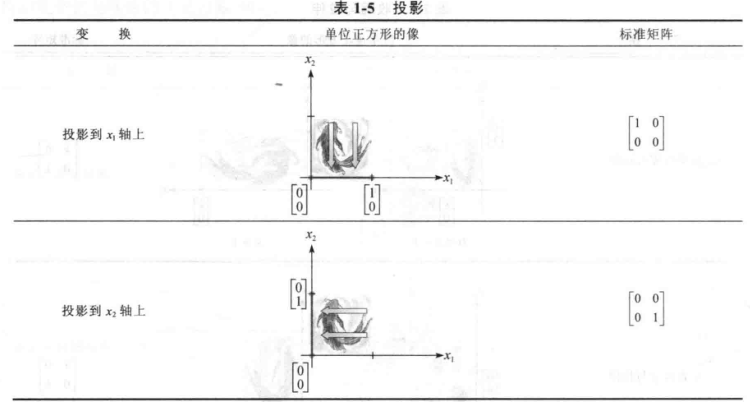
满射和单射

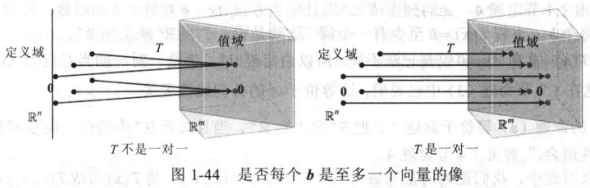
定理

• 设 T：$R^n \rightarrow R^m$ 为线性变换；
• 则 T 是一对一的当且仅当 Ax = 0 仅有平凡解；