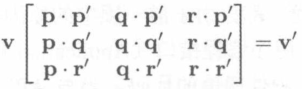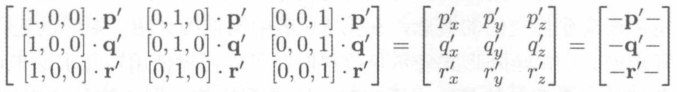三维旋转

定向

定向和方向的区别

• 方向可以使用两个参数表示 (极坐标)；
• 定向需要三个参数 (欧拉角)；

矩阵形式

矩阵的选择

矩阵的选择

• 使用直立空间坐标的表示的对象空间的正交基构成的 3 * 3 矩阵表示；

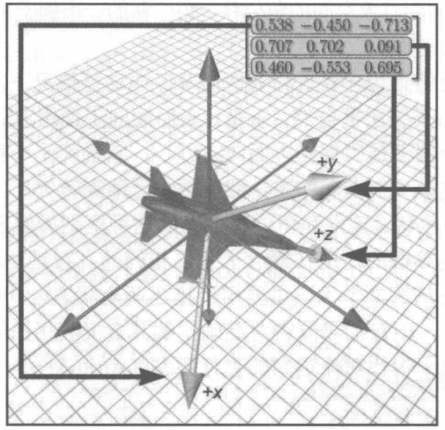
对象空间坐标和直立空间坐标的转换

• 假设对象空间坐标，直立空间坐标，旋转矩阵依次为 o，u，m；

$u = o \cdot m$ $o = u \cdot m^{-1}$

方向余弦矩阵

方向余弦矩阵和旋转矩阵的关系

• 两者相同；
• 方向余弦矩阵只是一种解释旋转矩阵的方式；

旋转矩阵的元素值

• 旋转矩阵元素值为当前空间对应轴与目标空间对应轴的点积；
• 若两个空间的基向量都为标准正交基；
  • 当前空间的基向量使用目标空间的基向量表示；
• 故旋转矩阵元素值为两个空间对应基向量的夹角；

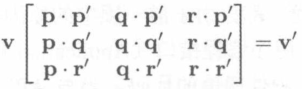
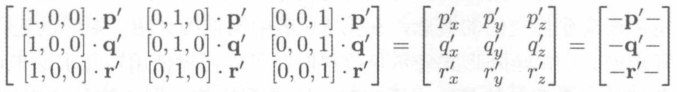
矩阵形式的优缺点

矩阵形式的优点

• 可以直接在对象空间和直立空间之间转换；
• 可以嵌套多个坐标之间的转化关系；
• 可以通过矩阵求逆反向计算；

矩阵形式的缺点

• 占用更多的空间，数据冗余；
• 人类难以使用；

欧拉角

欧拉角约定

欧拉角

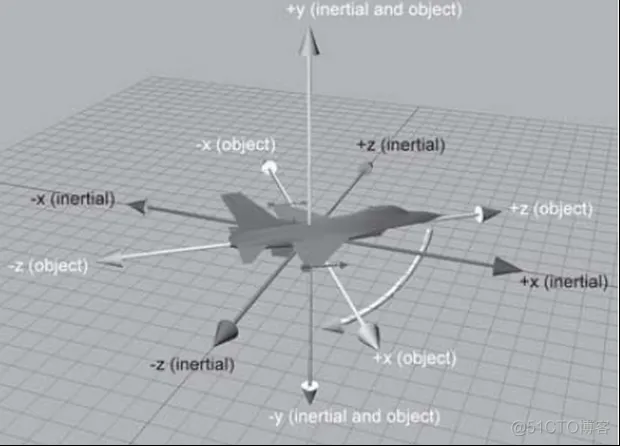
• 围绕对象空间 3 个垂直轴的三个夹角；
• 首先将对象空间和直立空间的轴对齐；
• 依次为航向角 (方位角)，俯仰角和翻滚角，即 +y，+x，+z 的夹角；
• 使用左手坐标系：+x 向右，+y 向上，+z 向前；
• 正方向使用左手旋转；

名称

• 航向角 - 俯仰角 - 翻滚角；
• Yaw-Pitch-Roll；
• Heading-Pitch-Bank；

固定轴

固定轴

• 旋转轴始终为直立空间的 3 个垂直轴；

旋转顺序

• 依次为翻滚角，俯仰角和航向角 (方位角)，即 +z，+x，+y 的夹角；
• 旋转顺序和欧拉角相反；
• 固定轴称其为外旋；
• 欧拉角称其为内旋；

欧拉角的优缺点

欧拉角的优点

• 易于人类使用；
• 数据容易压缩；
• 任意一组 3 个数字都有效；

欧拉角的缺点

• 定向的表示不是唯一的；
  • 角度可以任意添加 2pi；
  • 通过调整旋转顺序和旋转轴，可以得到不同的表示方法：万向节死锁；
• 两个定向之间的插值由于定向的表示不唯一，具有问题；

欧拉角的规范化

定向插值的优化公式

• 一定使用规范化的欧拉角；
• 限制旋转角度在 180 度；

轴-角和指数映射

欧拉旋转定理

• 任意两个定向 r1，r2；
• 都存在唯一的轴 n；
• 使得围绕 n 旋转一次即可从 r1 到 r2；

轴-角

• 设旋转角 $\theta$ 和过原点的旋转轴，该轴平行于单位向量 $\hat{n}$；

指数映射

• $e = \theta \hat{n}$ 为使用指数映射描述轴-角形式的角位移；
• $\theta = ||e||$；

四元数

四元数表示法

四元数表示法

• 标量分量 + 向量分量；
• [w，(x，y，z)]；
• [w，v]；

意义

$q = [w \quad v] = [\cos(\frac{\theta}{2}) \quad \sin(\frac{\theta}{2})\hat{n}]$ $q = [w \quad (x,y,z)] = [\cos(\frac{\theta}{2}) \quad \sin(\frac{\theta}{2})n_x \quad \sin(\frac{\theta}{2})n_y \quad \sin(\frac{\theta}{2})n_z]$

四元数变负

四元数变负

• -[w，(x，y，z)] = [-w，(-x，-y，-z)] = -[w，v] = [-w，-v]；
• 四元数变负表示相同的角位移；

单位四元数

单位四元数

• [1 0]；
• [-1 0]；

四元数的大小

四元数的大小

$||q|| = \sqrt{\omega^2 + x^2 + y^2 + z^2}$

四元数的共轭和逆

四元数的共轭

$q^* = [w \quad -v] = [w \quad (-x,-y,-z)]$

四元数的逆

$q^{-1}=\frac{q^*}{||q||}$ $q^{-1} \cdot q = [1,0]$

四元数乘法

四元数乘法

$q_1q_2 = [\omega_1 \quad v_1][\omega_2 \quad v_2] = [\omega_1\omega_2 - v_1 \cdot v_2 \quad \omega_1v_2 + \omega_2v_1 + v_1 \times v_2]$

四元数的结合律和交换律

$(ab)c = a(bc)$ $ab \neq ba$

四元数乘积的大小

$||q_1q_2||=||q_1||||q_2||$

四元数乘积的倒数

$(q_1 \cdots q_n)^{-1} = q_n^{-1}\ \cdots q_1^{-1}$

使用四元数乘法旋转三维矢量

• 设四元数 q 和三维向量 p；
• p 围绕 $\hat{n}$ 转换 $\theta$

$p'=qpq^{-1}$

四元数连接多个旋转

$p'=(q_1q_2)p(q_1q_2)^{-1}$

四元数的差

四元数的差

• 给定方向 a 和 b；
• 计算 a 到 b 旋转的角位移 d；

$da=b$ $d=ba^{-1}$

四元数点积

四元数点积

$q_1 \cdot q_2 = [\omega_1 \quad v_1][\omega_2 \quad v_2] = \omega_1\omega_2 + v_1 \cdot v_2$

四元数的对数, 指数和标量乘法

使用半角定义四元数

$\alpha = \frac{\theta}{2} \qquad q = [\cos\alpha \quad \hat{n}\sin\alpha]$

四元数的对数

$logq = log([\cos\alpha \quad \hat{n}\sin\alpha]) \equiv [0 \quad \alpha\hat{n}]$

四元数的指数函数

$expp=exp([0 \quad \alpha\hat{n}]) = [\cos\alpha \quad \hat{n}\sin\alpha]$

四元数对数和指数的性质

$exp(logq)=q$

四元数乘以标量

$kq=k[\omega v]=[k\omega kv]$

四元数指数

四元数指数

$q^t$

最短弧

• 四元数使用最短弧表示角度位移；
• 若 q 为绕 x 轴顺时针旋转 30 度；
• q^8 并不是绕 x 轴顺时针旋转 240 度，而是 绕 x 轴逆时针旋转 120 度；

四元数取幂公式

$q^t=exp(tlogq)$

四元数插值

理论上的四元数 Slerp 公式

$slerp(q_0,q_1,t)=(q_1q_0^{-1})^tq_0$

实际的四元数 Slerp 公式

$slerp(q_0,q_1,t)=\frac{\sin(1-t)\omega}{\sin\omega}q_0+\frac{\sin t\omega}{\sin\omega}q_1$

四元数的优缺点

优点

• 平滑插值；
• 角位移的快速连接和逆；
• 矩阵形式的快速转换；
• 仅有四个数字；

缺点

• 存储空间略大于欧拉角；
• 可能无效；
• 人类难以使用；

四元数概要

四元数概要

• 四元数通过旋转轴和围绕旋转轴的量表示角位移；
• 四元数包括标量分量和向量分量；
• 三维的每个角位移具有两种不同的四元数表示，两者互为倒数；
• 表示无角度的四元数为单位四元数；
• 所有表示角位移的四元数都是单位四元数，大小为 1；
• 四元数的共轭表示相反的角位移；
• 四元数乘法可以链接多个旋转；
• 四元数取幂用于计算角位移的倍数，总是采用最短的弧；

表示方法之间的转换

基础

总览

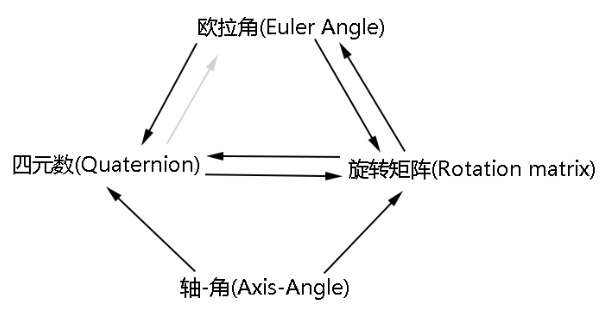
欧拉角和矩阵的转换

欧拉角转换为对象空间到直立空间的旋转矩阵

• 使用固定轴旋转；

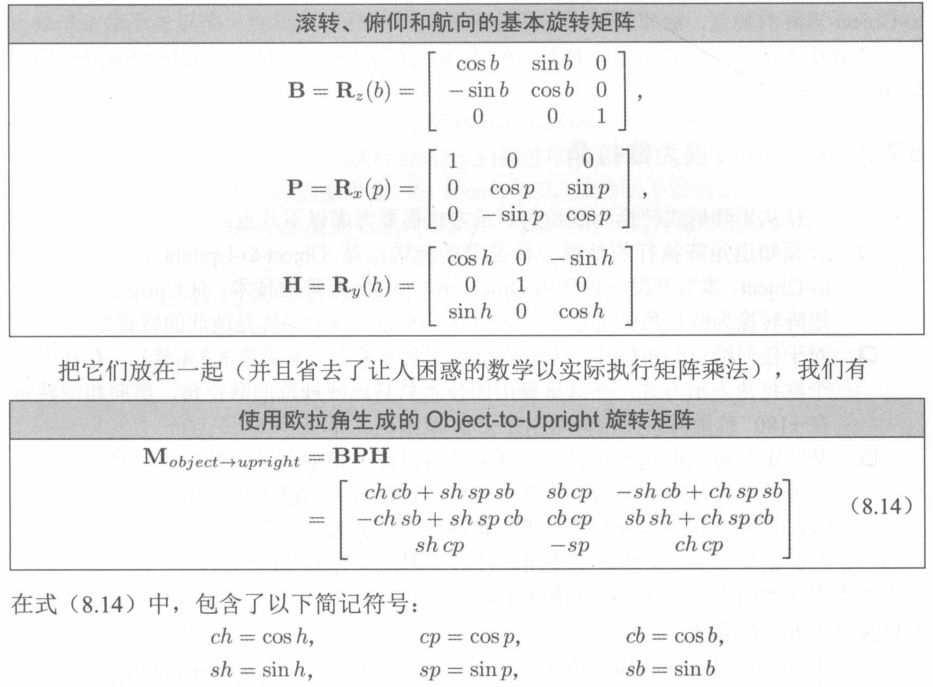
欧拉角转换为直立空间到对象空间的旋转矩阵

• 使用固定轴旋转；
• 对象空间到直立空间的转换的旋转矩阵的转置矩阵；

矩阵转换为欧拉角

$p = \arctan2(-m_{32})$ $h = \arctan2(m_{31}, m_{33})$ $b = \arctan2(m_{12}, m_{22})$

四元数和矩阵的转换

四元数转换为矩阵

矩阵转换为四元数

• 选择绝对值最大的作为起始值；

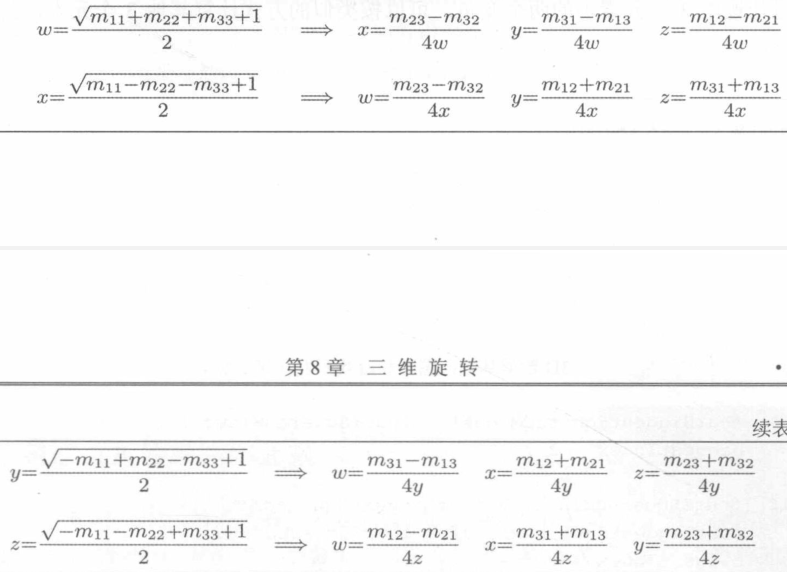
欧拉角和四元数的转换

欧拉角转换为对象空间到直立空间的四元数

欧拉角转换为直立空间到对象空间的四元数

• 欧拉角转换为对象空间到直立空间的四元数求共轭；

四元数转换为欧拉角