笛卡尔坐标系

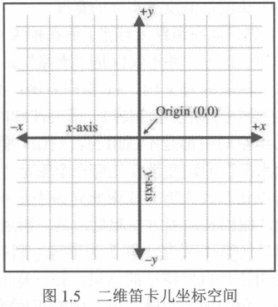
二维笛卡尔空间

二维笛卡尔坐标系

计算机屏幕坐标系

笛卡尔坐标

• (x，y) 分别指定 x 轴和 y 轴的投影位置；

三维笛卡尔空间

三维笛卡尔坐标空间

三维笛卡尔坐标

• (x，y，z) 分别指定 x 轴，y 轴和 z 轴的投影位置；

左手坐标系和右手坐标系

• 相同种类的坐标系可以通过旋转使轴对齐；
• 拇指，食指和中指分别指向 x，y，z；

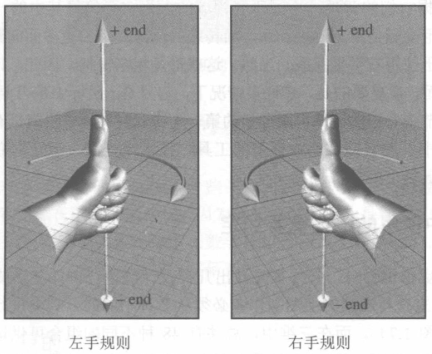
左手规则和右手规则

• 规定旋转的正方向；
• 拇指指向旋转轴的正方向；
• 手指弯曲方向即正方向；

基本约定

• 使用左手坐标系和左手规则；

其他

求和和求积的表示法

求和表示法

$\sum^n_{i=1}a_i = a_1 + \cdots + a_n$

求积表示法

$\prod^n_{i=1}a_1 = a_1 \times \cdots \times a_n$

区间符号

区间符号

$[a,b]\qquad a \le x \le b$ $(a,b)\qquad a \lt x \lt b$ $[a,b)\qquad a \le x \lt b$ $(a,b]\qquad a \lt x \le b$

角度, 度数和弧度

$360\degree = 2 \pi \ rad$

三角函数

三角函数定义

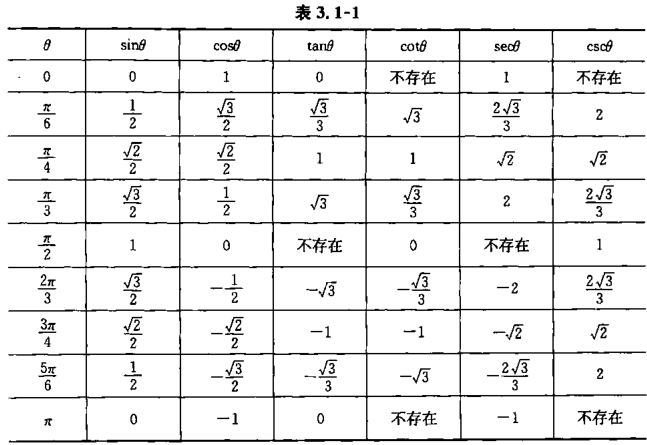
三角函数特殊值

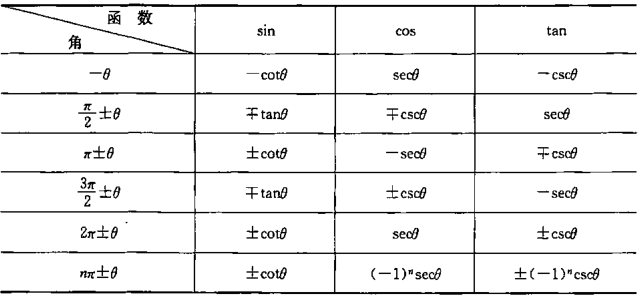
任意三角函数诱导公式

• 通用解法：奇变偶不变，符号看象限；
• 奇变偶不变；
  • 当 k 为偶数是，三角函数符号不变；
  • 当 k 为奇数是，三角函数符号翻转对应形式；
• 符号看象限；
  • 计算 $\frac{k}{2}\pi + \alpha$ 对应角度所在象限；
  • 三角函数的正负号即原三角函数符号对应的角度在该象限的正负值；

$sin(\frac{k}{2}\pi + \alpha)$

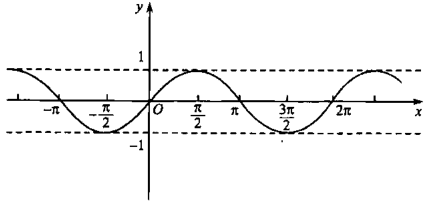
sin

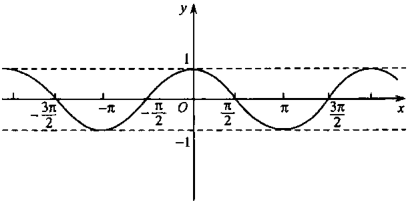
cos

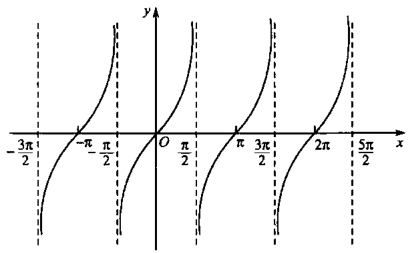
tan

cot

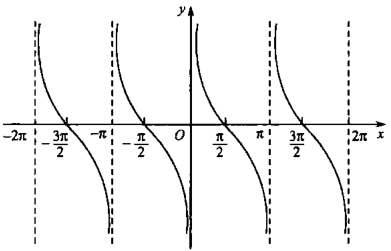
sec

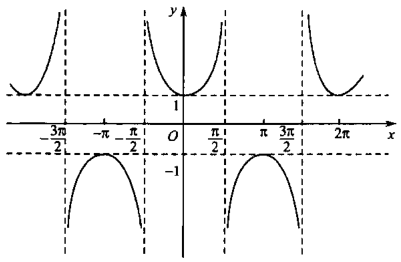
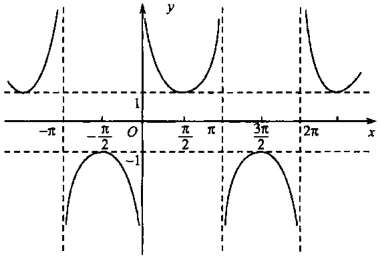
csc

两角和公式

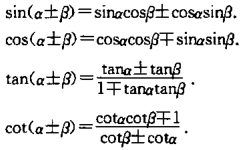
倍角公式

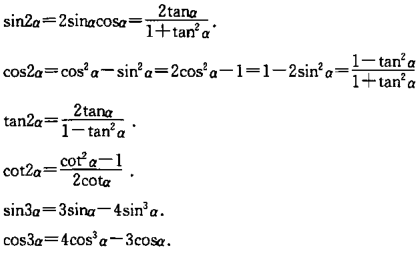
半角公式

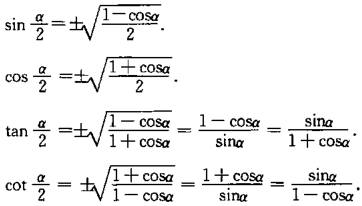
和差化积

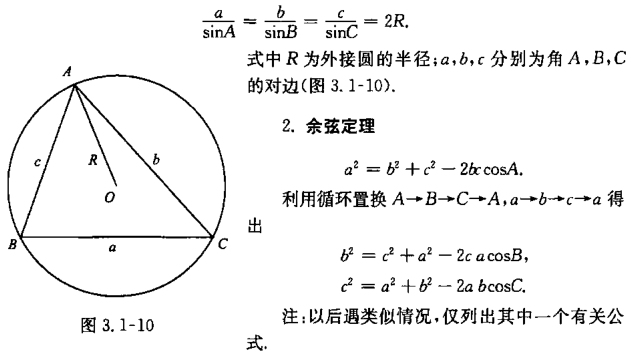
正弦定理和余弦定理