几何图元

表示形式

隐含形式

$x^2+y^2+z^2=1$

参数形式

$x(t)=\cos2\pi t \qquad y(t)=\sin2\pi t$

线

直线

向量定义

$p(t)=p_0+tu$

光线

光线

• 与射线不同；
• 图形学中的光线为有向线段；

向量定义

• d 有方向和大小；

$p(t)=p_0+td \qquad t\in[0,1]$

线段

几何定义

• [p1，p2]；

球和圆

球和圆

• 中心为 c，半径为 r；
• c 和 p 皆为向量；

$||p-c||=r$

初等几何公式

$D=2r$ $C=2\pi r$ $A = \pi r^2$ $S = 4 \pi r^2$ $V=\frac{4}{3}\pi r^3$

AABB

AABB 的表示形式

向量表示

$p_{min}=[x_{min},y_{min},z_{min}] \qquad p_{max}=[x_{max},y_{max},z_{max}]$

计算 AABB

计算过程

• 首先将 p_min 设置为正无穷大和 p_max 设置为负无穷大；
• 根据各点依次比较；

for (let index = 0; index < length; index++) {
  const vertex = vertices[index];
  const [x, y, z] = vertex.get();
  if (x < minX) minX = x;
  if (y < minY) minY = y;
  if (z < minZ) minZ = z;
  if (x > maxX) maxX = x;
  if (x > maxY) maxY = y;
  if (z > maxZ) maxZ = z;
}

AABB 和包围球

AABB 的优点

• AABB 易于实现，计算速度高；
• AABB 有三个自由度，包围球只有一个自由度；

变换 AABB

变换原理

• 对 AABB 4 个顶点进行旋转；
• 基于旋转前的 4 个顶点和旋转后的 4 个顶点 (8 个顶点) 计算一个新的 AABB；

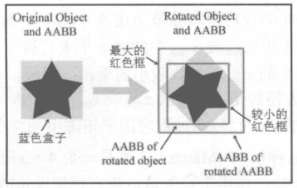
快速算法

• 基于 AABB 的结构加快运算；
• 以 x_min 为例；
  • 若想下述公式总和最小，要求 3 个乘积都为最小；
    • 若 m11 > 0，取 x_min，反之取 x_max；
    • 若 m21 > 0，取 y_min，反之取 y_max；
    • 若 m31 > 0，取 z_min，反之取 z_max；
  • x，y，z 根据上述步骤以此类推；

$x=m_{11}x+m_{21}y+m_{31}z$

平面

平面方程

向量表示

• p 为平面一点；
• n 为平面法线；
• d 为平面到原点距离；

$p\cdot n = d$

三点定义一个平面

$e_1=p_2-p_1 \quad e_2 = p_3-p_2 \quad \hat{n} = \frac{e_1 \times e_2}{||e_1 \times e_2||}$

超过三个点的最佳拟合平面

$n_x=\sum^n_{i=1}(y_i-y_{i+1})(z_i+z_{i+1})$ $n_y=\sum^n_{i=1}(z_i-z_{i+1})(x_i+x_{i+1})$ $n_z=\sum^n_{i=1}(x_i-x_{i+1})(y_i+y_{i+1})$ $d=\frac{1}{n}(\sum^n_{i+1}p_i)\hat{n}$

三角形

向量表示

• 顺时针表示 3 个顶点；

中心坐标

• 中线交点；

$\frac{v_1+v_2+v_3}{3}$

内心坐标

• 角平分线交点；
• l 为 v 对应的边；

$\frac{l_1v_1 + l_2v_2 + l_3v_3}{l_1 + l_2 + l_3}$

外心坐标

• 垂直平分线交点；
• 太长了记不住，用的时候 google；

多边形

简单多边形

• 无孔的多边形；

复杂多边形

• 有孔的多边形；

自相交多边形

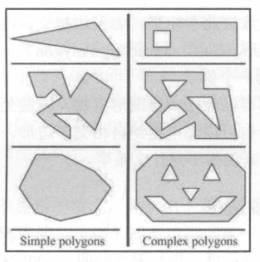
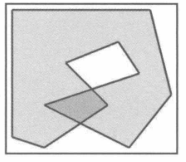
• 边相交的多边形；

凸多边形和凹多边形

• 凸多边形中的任意两点之间的直线完全在多边形内；
• 凸多边形沿边移动，顶点朝一个方向旋转；

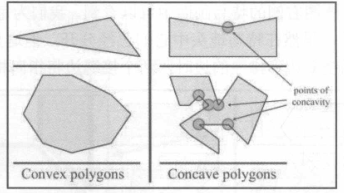
凸多边形的判断

• 凸多边形的内角和为 (n-2)*180 度；

三角剖分

• 非常复杂，简单的凸多边形可以使用扇形分割代替；