空间数据结构
基本概念
数据结构
- 数据组织的形式;
- 适合于计算机管理,分析;
空间数据结构内容
- 空间;
- 属性;
- 空间关系;
空间数据结构
- 矢量数据结构;
- 栅格数据结构;
- 一体化数据结构;
- 镶嵌数据结构;
- 多维数据结构;
矢量数据结构
基本概念
矢量数据结构
- 记录实体坐标及其空间关系;
- 精确定义空间实体;
文件结构
| 标识码 | 属性 |
|---|---|
分类
- 实体数据结构;
- 拓扑数据结构;
- 网络数据结构;
实体数据结构
实体数据结构 (spaghetti 数据结构)
- 以多边形为单元;
- 记录各多边形的各线段;
缺点
- 公共边重复记录,数据冗余;
- 无法表示空间关系;
拓扑数据结构
基本概念
拓扑数据结构
- 具有拓扑关系的数据结构;
- 点相互独立;
- 点连成线,线构成面;
- 线始于起始结点,止于终止结点,与左右多边形邻接;
分类
- 索引式数据结构;
- 双重独立编码;
- 链式双重独立编码;
索引式数据结构
- 采用树状索引;
- 点顺序存储;
- 点文件 + 边文件 + 多边形文件;
双重独立编码结构 (DIME)
- 以线段为单元;
- 顺序记录线段两点和相邻多边形;
- 点文件 + 线段拓扑关系文件 + 多边形文件;
链式双重独立数据结构
- 对 DIME 数据结构的改进;
- 将若干条线段合并为一个弧段;
- 点文件 + 弧点文件 + 弧段拓扑关系文件 + 多边形文件;
网络数据结构
- 记录相连的边和交汇点;
- 点文件 + 边文件 + 点边拓扑关系关系文件;
栅格数据结构
基本概念
栅格数据结构
- 规则栅格矩阵;
- 行列号确定位置;
- 栅格值表示属性且取值唯一;
分类
- 完全栅格结构;
- 压缩栅格结构;
- 链码结构;
- 瓦片金字塔;
完全栅格数据结构
完全栅格数据结构
- 规则栅格矩阵;
- 逐行逐个记录栅格单元值;
- 不采用任何数据压缩处理;
压缩栅格数据结构
游程长度编码结构
游程长度编码结构
- 逐行逐列扫描栅格矩阵;
- 当栅格值发生变化时;
- 记录该值及其相同值重复个数;
文件结构
| (s, li) |
|---|
| (1, 5)(3, 3) |
| (2, 3)(6, 5) |
| (1, 4)(2, 1)(7, 3) |
四叉树数据结构
四叉树数据结构
- 栅格矩阵递归四等分;
- 直至每个子块各格网值相同或不可分割;
常规四叉树
- 四个叶结点 + 父结点指针 + 叶结点属性值;
线性四叉树
- 叶结点地址码 (十进制 Morton 码) + 叶结点属性值;
十进制 Morton 码计算
- 行列号转换为二进制 (行列号从 0 开始);
- 构造二进制 Morton 码;
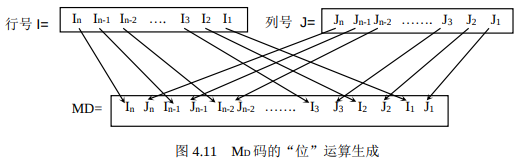
- 二进制 Morton 码转换为十进制;
文件结构
| Morton 码 | 属性值 |
|---|---|
| 0 | 2 |
| 4 | 3 |
| 7 | 5 |
二维行程编码结构
- 若线性四叉树前后叶结点属性值相同;
- 则归并前后叶结点;
链码结构
采用弗里曼码编码;
瓦片金字塔结构
- 金字塔结构;
- 不同分辨率栅格数据分层存储;
- 有损压缩方式;
矢量与栅格数据结构
矢量数据与栅格数据结构的比较
| 优点 | 缺点 | |
|---|---|---|
| 矢量数据结构 | 数据结构严密; 数据冗余度小; 数据量小; 拓扑关系清晰; 图形质量和精度高 | 数据结构算法复杂; 空间分析复杂; 输出方法复杂 |
| 栅格数据结构 | 数据结构简单; 空间分析简单; 输出方法简单 | 数据冗余度大; 数据量大; 难以建立拓扑关系; 图形质量和精度低 |
矢量数据与栅格数据结构的转化
矢量数据到栅格数据的结构转换
基本前提
- 确定栅格大小:数据输出精度;
- 栅格值计算原则:单个栅格存在多个对象,栅格值的计算方式;
- 平均值;
- 总和;
- 最值;
点的转换
- 通过转换公式;
线的转换
- 八方向栅格化法;
面的转换 (多边形填充)
- 内部点扩散法;
- 射线法;
- 扫描线法;
栅格数据到矢量数据的结构转换
点的转换
- 通过转换公式;
线的转换
- 二值化;
- 确定阀值;
- 小于阀值取 0,反之取 1;
- 矢量化;
- 细化;
- 跟踪;
- 八邻域搜索;
- 坐标变化;
- 拓扑化;
面的转换
- 仅需进行轮廓线的转化,等同于线的转化;
矢量栅格一体化结构
- 多级格网 (栅格):粗格网 + 基本格网 + 细分格网;
- 线性四叉树编码 (栅格):(M1,M2,M3),M 表示点或线经过各格网的 Morton 码;
- 三个基本约定 (矢量):点线面之间的拓扑关系;
镶嵌数据结构
规则镶嵌数据结构
规则镶嵌数据结构
- 栅格数据结构;
不规则镶嵌数据结构
- Voronoi 数据结构;
- TIN 数据结构;
多维数据结构
八叉树数据模型
- 四叉树在三维空间的推广;
- 三维空间 X,Y,Z 三个方向递归八等分;
- 直至每个子块各格网值相同或不可分割;
三维边界表示法
- 顶点位置;
- 构成边的顶点;
- 构成面的边;