动态规划
基础
基本思想
- 将问题分解为子问题;
- 通过存储子问题的解,避免重复计算;
基本术语
- dp 表:记录子问题的解;
- 初始状态:最小子问题的状态;
- 状态转移公式:dp 的递推公式;
dp 问题特性
最优子结构
- 原问题的最优解,是从子问题的最优解构建得来;
无后效性
- 给定确定状态;
- 未来状态只和当前状态有关,与过去状态无关;
- 存在严重后效性的问题,难以使用动态规划解决;
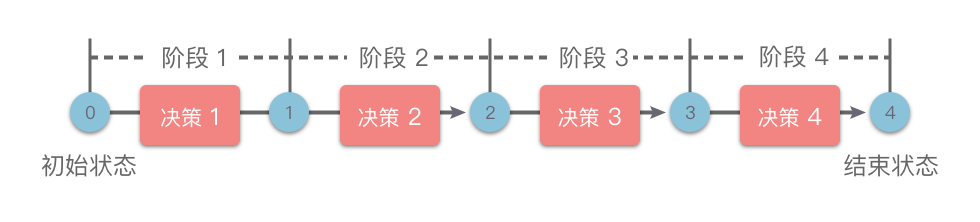
dp 解题思路
- 划分阶段;
- 将问题按照特定顺序分解为互相联系的阶段,即子问题的求解;
- 完成前一阶段才可进行下一阶段;
- 定义状态:根据问题变量设置状态,建立 dp 表;
- 状态转移:建立不同阶段之间的状态转移公式;
- 初始条件和边界条件:确定初始条件和边界条件;
动态规划基础题目
斐波那契数
题目
- 509;
思路
- 划分阶段:根据整数顺序进行划分;
- 定义状态:dp[i] 为第 i 个斐波那契数;
- 状态转移方程:dp[i] = dp[i-1] + dp[i-2];
- 初始条件:dp[0]=0,dp[1]=1;
- 边界条件:i===n;
/**
* @param {number} n
* @return {number}
*/
var fib = function (n) {
const dp = new Array(n + 1);
dp[0] = 0;
dp[1] = 1;
for (let i = 2; i < n + 1; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
};
复杂度
- 时间:n;
- 空间:n;
爬楼梯
题目
- 70;
思路
- 划分阶段:根据楼梯阶层划分为 0 - n;
- 定义状态:dp[i] 为爬到第 i 阶的方案数;
- 状态转移方程;
- 设爬到第 i 阶有 dp[i] 种方案;
- 由于只能上 1 阶或 2 阶;
- 因此第 i 阶的上一轮只能在 i - 1 阶或 i-2 阶上;
- 故 dp[i] = dp[i-1] + dp[i-2];
- 初始条件:dp[1]=1,dp[2]=2
/**
* @param {number} n
* @return {number}
*/
var climbStairs = function (n) {
const dp = new Array(n + 1);
dp[1] = 1;
dp[2] = 2;
for (let i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
};
复杂度
- 时间:n;
- 空间:n;
圆环回原点问题
题目
- 圆环上有 10 个点,编号为 0~9,从 0 点出发,每次可以逆时针和顺时针走一步,问走 n 步回到 0 点共有多少种走法;
思路
- 划分阶段:根据步数和到达位置划分;
- 定义状态:dp[n][index] 为走 n 步到达 index 位置的走法数量;
- 状态转移方程;
- index 只能从 index-1 和 index+1 走来;
- dp[n][index] = dp[n-1][(index+1)%len]+dp[n-1][(index-1+len)%len];
- 初始条件;
- dp[0][0]=1;
- 终止条件:到达 [m-1,n-1];
class Solution:
def backToOrigin(self,n):
length = 10
dp = [[0 for i in range(length)] for j in range(n+1)]
dp[0][0] = 1
for i in range(1,n+1):
for j in range(length):
dp[i][j] = dp[i-1][(j-1+length)%length] + dp[i-1][(j+1)%length]
return dp[n][0]
复杂度
- 时间:n2;
- 空间:n2;
不同路径 1
题目
- 62;
思路
- 划分阶段:根据行列号进行划分;
- 定义状态:dp[row][col] 为到达该点不同路径数量;
- 状态转移方程;
- 只能向下,向右移动;
- dp[row][col] = dp[row-1][col] + dp[row][col-1];
- 初始条件;
- 左上角至 [0,0] 数量为 1,故 dp[0][0] = 1;
- 左上角至首行首列数量为 1,故 dp[0][:] = dp[:][0] =- 1;
- 终止条件:到达 [m-1,n-1];
/**
* @param {number} m
* @param {number} n
* @return {number}
*/
var uniquePaths = function (m, n) {
const dp = new Array(m).fill(0).map(() => new Array(n).fill(1));
for (let row = 1; row < m; row++) {
for (let col = 1; col < n; col++) {
dp[row][col] = dp[row - 1][col] + dp[row][col - 1];
}
}
return dp[m - 1][n - 1];
};
复杂度
- 时间:mn;
- 空间:mn;
不同路径 2
题目
- 63;
思路
- 划分阶段:根据行列号进行划分;
- 定义状态:dp[row][col] 为到达该点不同路径数量;
- 状态转移方程;
- 只能向下,向右移动;
- dp[row][col] = dp[row-1][col] + dp[row][col-1];
- 如果 dp[row][col]为障碍物,赋值为 0;
- 初始条件;
- 左上角至 [0,0] 数量为 1,故 dp[0][0] = 1;
- 左上角至首行首列数量为 1,故 dp[0][:] = dp[:][0] = 1;
- 如果在首行首列遇到障碍,跳出循环;
- 终止条件:到达 [m-1,n-1];
/**
* @param {number[][]} obstacleGrid
* @return {number}
*/
var uniquePathsWithObstacles = function (obstacleGrid) {
const m = obstacleGrid.length;
const n = obstacleGrid[0].length;
const dp = Array.from(
{
length: m,
},
() => new Array(n).fill(0)
);
for (let i = 0; i < m; i++) {
if (obstacleGrid[i][0] === 1) break;
dp[i][0] = 1;
}
for (let i = 0; i < n; i++) {
if (obstacleGrid[0][i] === 1) break;
dp[0][i] = 1;
}
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
if (obstacleGrid[i][j] === 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
};
复杂度
- 时间:mn;
- 空间:mn;
不同的二叉搜索树
题目
- 96;
思路
- 数学题,建议死记硬背;
- f[i] 表示以 i 为根的二叉搜索树的个数,g[i] 表示 i 个节点可以构成的个数;
- g[i]=f[1]+f[2]+。。。+f[i];
- i 为根节点时,使用 i - 1 个节点构造左树,n- i 个节点构造右树,f[i]=g[i-1]*g[n-i];
- 综上
- 划分阶段:根据节点索引划分;
- 定义状态:dp[i]表示 i 个节点可以构成的二叉树数量;
- 状态转移公式:g[i] 换 dp[i];
- 起始条件:dp[0]=1,即空树;
- 终止条件,返回 dp[n];
/**
* @param {number} n
* @return {number}
*/
var numTrees = function (n) {
const dp = new Array(n + 1).fill(0);
dp[0] = 1;
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
};
复杂度
- 时间:n^2;
- 空间:n;
记忆化搜索
记忆化搜素
- 存储已经遍历过的状态信息;
- 计算子问题时判断对应状态是否存储;
记忆化搜素和递推
- 记忆化搜索;
- 自顶向下,自然的递归方式;
- 简单易懂;
- 存在栈溢出问题;
- 递推;
- 自底向上;
- 不存在栈溢出问题;
- 无法处理复杂的状态转移方程;
解题步骤
- 定义状态和状态转移方程;
- 定义数组缓存子问题解;
- 定义递归函数,首先检查缓存是否存在对应的解;
记忆化搜索题目
矩阵中的最长递增路径
题目
- 329;
思路
- 对于每个单元格,可以上下左右移动;
- 遍历过的单元格不在遍历;
- 二维数组存储当前单元格的最大路径长度;
/**
* @param {number[][]} matrix
* @return {number}
*/
var longestIncreasingPath = function (matrix) {
const dirctionList = [
[0, 1],
[0, -1],
[1, 0],
[-1, 0],
];
const dfs = (matrix, row, col, rows, cols, memo) => {
if (memo[row][col] !== 1) return memo[row][col];
let max = 1;
for (const [dx, dy] of dirctionList) {
const curRow = row + dx;
const curCol = col + dy;
if (
curCol < 0 ||
curCol >= cols ||
curRow < 0 ||
curRow >= rows ||
matrix[curRow][curCol] <= matrix[row][col]
)
continue;
max = Math.max(max, 1 + dfs(matrix, curRow, curCol, rows, cols, memo));
}
memo[row][col] = max;
return max;
};
if (matrix.length === 0) return 0;
const m = matrix.length;
const n = matrix[0].length;
const memo = Array.from(
{
length: m,
},
() => new Array(n).fill(1)
);
let res = 1;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
res = Math.max(res, dfs(matrix, i, j, m, n, memo));
}
}
return res;
};
复杂度
- 时间:n^2;
- 空间:n^2;
线性 dp
线性 dp
- 具有线性阶段划分的动态规划方法;
- 根据输入方法划分;
- 单串线性 dp;
- 双串线性 dp;
- 矩阵线性 dp;
- 无串线性 dp;
单串线性 dp
概述
- 问题输入为单个数组或单个字符串;
- 状态一般定义为 dp[i];
- nums[i] 结尾的子数组的相关状态;
- nums[i-1] 结尾的子数组的相关状态;
子数组和子序列
- 子序列:不改变数组原有顺序的元素序列,可不连续;
- 状态一般是前 i 个元素;
- 子数组:数组中的连续子序列;
- 状态一般是以 nums[i] 结尾;
双串线性 dp 问题
- 问题输入为两个数组或两个字符串;
- 状态一般定义为 dp[i][j];
- nums1[i] 和 nums2[j] 结尾的子数组的相关状态;
- nums2[i-1] 和 nums2[j] 结尾的子数组的相关状态;
矩阵线性 dp 问题
- 问题输入为二维矩阵;
- 状态一般定义为 dp[i][j],表示从 [0,0] 到 [i,j] 的相关状态;
无串线性 dp 问题
- 问题输入不是显式的数组,字符串或矩阵;
- 但可以分解为若干子问题的线性 dp 问题;
线性 dp 题目
最长递增子序列
题目
- 300;
思路
- 划分阶段:根据子序列末端索引划分;
- 定义状态:dp[i] 即以 nums[i] 结尾的最长递增子序列长度;
- 状态转移方程;
- 对于任意
0 <= j < i; - 若 nums[i]>nums[j],dp[i] = dp[j] + 1,反之为 1;
- 即
dp[i] = max(dp[i],dp[j]+1), (0 <= j < i, nums[i]>nums[j]);
- 对于任意
- 初始条件:默认每个状态皆为长度为 1 的递增子序列;
- 终止条件:返回 max(dp);
/**
* @param {number[]} nums
* @return {number}
*/
var lengthOfLIS = function (nums) {
const dp = new Array(nums.length).fill(1);
for (let i = 1; i < nums.length; i++) {
for (let j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
return Math.max(...dp);
};
复杂度
- 时间:n^2;
- 空间:n;
最长递增子序列的个数
题目
- 673;
思路
- 求最长递增子序列思路同最长递增子序列;
- 定义状态:额外定义 count[i],表示第 i 个字符前,最长递增子序列的个数;
- 状态转移公式;
- 如果 dp[j]+1>dp[i],表示第一次找到 dp[j]+1 长度的子序列,count[i]=count[j];
- 如果 dp[j]+1=dp[i],表示当前长度已经找到,组合数相加,count[i]+=count[j];
- 起始条件:count[i]=1;
- 终止条件:到达数组末端;
- 首先获取最长递增子序列长度;
- 获得该长度的组合数;
/**
* @param {number[]} nums
* @return {number}
*/
var findNumberOfLIS = function (nums) {
const dp = new Array(nums.length).fill(1);
const count = new Array(nums.length).fill(1);
for (let i = 1; i < nums.length; i++) {
for (let j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
if (dp[j] + 1 > dp[i]) {
dp[i] = dp[j] + 1;
count[i] = count[j];
} else if (dp[j] + 1 === dp[i]) {
count[i] += count[j];
}
}
}
}
let res = 0;
const max = Math.max(...dp);
for (let i = 0; i < count.length; i++) {
if (dp[i] === max) res += count[i];
}
return res;
};
复杂度
- 时间:n^2;
- 空间:n;
俄罗斯套娃信封问题
题目
- 354;
思路
- 根据宽度对信封进行升序排列,相同宽度根据高度降序排列;
- 然后问题就转变为对信封高度求最长递增子序列;
- 使用动态规划会超时,所以使用二分查找方法;
/**
* @param {number[][]} envelopes
* @return {number}
*/
var maxEnvelopes = function (envelopes) {
envelopes = envelopes.sort((a, b) => {
if (a[0] === b[0]) return b[1] - a[1];
return a[0] - b[0];
});
const minStack = [envelopes[0][1]];
for (let i = 1; i < envelopes.length; i++) {
const num = envelopes[i][1];
if (num > minStack[minStack.length - 1]) {
minStack.push(num);
} else {
let left = 0;
let right = minStack.length;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
if (num < minStack[mid]) right = mid;
else if (num === minStack[mid]) right = mid;
else if (num > minStack[mid]) left = mid + 1;
}
minStack[left] = num;
}
}
return minStack.length;
};
复杂度
- 时间:n^2;
- 空间:n;
最大子数组和
题目
- 53;
思路
- 划分状态:根据子数组末端索引划分;
- 定义状态:dp[i] 为第 i 个数结尾的连续子数组的最大和;
- 状态转移方程;
- 如果
dp[i-1]<0,dp[i-1]+nums[i] 必然小于 nums[i]; - 反之必然大于 nums[i];
- 如果
- 初始条件:dp[0] = 0;
- 终止条件:达到数组末端,返回 dp[i];
/**
* @param {number[]} nums
* @return {number}
*/
var maxSubArray = function (nums) {
const dp = new Array(nums.length + 1);
dp[0] = 0;
for (let i = 0; i < nums.length; i++) {
if (dp[i] > 0) dp[i + 1] = dp[i] + nums[i];
else dp[i + 1] = nums[i];
}
dp.shift();
return Math.max(...dp);
};
复杂度
- 时间:n;
- 空间:n;
最长公共子序列
题目
- 1143;
思路
- 划分阶段:根据两个字符串结尾索引划分;
- 定义状态:dp[i][j] 表示为 t1 前 i 个元素和 t2 前 j 个元素的最长公共子序列长度;
- 状态转移方程;
- 双重遍历两个字符串;
- 维护最大 dp[i][j],记作 res;
- 若 t1[i-1] === t2[j-1],即两个字符串最后一位相同 dp[i][j] = dp[i-j][j-1]+1;
- 反之两个字符串最后一位不相同,dp[i][j] = max(dp[i-1][j],dp[i][j-1])
- 初始条件:d[0][j] = dp[j][0] = 0;
- 终止条件:双重遍历结束,返回 res;
/**
* @param {string} text1
* @param {string} text2
* @return {number}
*/
var longestCommonSubsequence = function (text1, text2) {
const dp = new Array(text1.length + 1)
.fill(0)
.map(() => new Array(text2.length + 1).fill(0));
for (let i = 1; i < text1.length + 1; i++) {
for (let j = 1; j < text2.length + 1; j++) {
if (text1[i - 1] === text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[text1.length][text2.length];
};
复杂度
- 时间:mn;
- 空间:mn;
最长重复子数组
题目
- 718;
思路
- 划分阶段:根据两个字符串结尾索引划分;
- 定义状态:dp[i][j] 表示为 t1 第 i 个元素为末尾项和 t2 第 j 个元素为末尾项的最长公共子数组长度;
- 状态转移方程;
- 双重遍历两个字符串;
- 维护最大 dp[i][j],记作 res;
- 若 t1[i-1] === t2[j-1],即两个字符串最后一位相同 dp[i][j] = dp[i-j][j-1]+1;
- 反之两个字符串最后一位不相同,dp[i][j] = 0;
- 初始条件:d[0][j] = dp[j][0] = 0;
- 终止条件:双重遍历结束,返回 res;
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number}
*/
var findLength = function (nums1, nums2) {
const m = nums1.length;
const n = nums2.length;
const dp = Array.from({ length: m + 1 }, () => new Array(n + 1).fill(0));
let res = 0;
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (nums1[i - 1] === nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = 0;
}
res = Math.max(res, dp[i][j]);
}
}
return res;
};
复杂度
- 时间:mn;
- 空间:mn;
编辑距离
题目
- 72;
思路
- 划分阶段:根据两个字符串结尾索引划分;
- 定义状态:dp[i][j] 表示为 s 的前 i 个字符修改为 t 的前 j 个字符,需要的最小编辑步数;
- 状态转移方程;
dp[i,j]中,对应字符为s[i-1],t[j-1];- 若 s[i-1] === t[j-1],无需任何操作,dp[i,j]=dp[i-1,j-1];
- 反之,三种操作对应三种情况;
- 添加:对应状态为
dp[i-1,j] + 1; - 删除:对应状态为
dp[i,j-1] + 1; - 替换:对应状态为
dp[i-1,j-1] + 1;
- 添加:对应状态为
- 初始条件;
- word1 前 0 个字符插入 j 次变为 word2 前 j 个字符:dp[0][j] = j;
- 同理删除 i 次 dp[i][0]=i;
- 终止条件:双层遍历完毕,返回 dp[-1][-1];
动态规划
/**
* @param {string} word1
* @param {string} word2
* @return {number}
*/
var minDistance = function (word1, word2) {
const dp = Array.from(
{ length: word1.length + 1 },
() => new Array(word2.length + 1)
);
for (let i = 0; i < word1.length + 1; i++) {
dp[i][0] = i;
}
for (let i = 0; i < word2.length + 1; i++) {
dp[0][i] = i;
}
for (let i = 1; i < word1.length + 1; i++) {
for (let j = 1; j < word2.length + 1; j++) {
if (word1[i - 1] === word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1;
}
}
}
return dp[word1.length][word2.length];
};
复杂度
- 时间:mn;
- 空间:mn;
最小路径和
题目
64;
思路
- 划分阶段:根据行列号进行划分;
- 定义状态:dp[row][col] 为到达该点的最小路径和;
- 状态转移方程;
- 只能向下,向右移动;
- dp[row][col] = min(dp[row-1][col],dp[row][col-1]) + grid[row][col];
- 初始条件;
- 显然 dp[0][0] = grid[0][0];
- 左上角至首行首列只能向左或向下;
- dp[row][0] = dp[row-1][0] + grid[row][col];
- dp[0][col] = dp[0][col-1] + grid[row][col];
- 终止条件:到达 [m-1,n-1];
/**
* @param {number[][]} grid
* @return {number}
*/
var minPathSum = function (grid) {
const rows = grid.length;
const cols = grid[0].length;
const dp = Array.from({ length: rows }, () => new Array(cols));
dp[0][0] = grid[0][0];
for (let i = 1; i < rows; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (let i = 1; i < cols; i++) {
dp[0][i] = dp[0][i - 1] + grid[0][i];
}
for (let i = 1; i < rows; i++) {
for (let j = 1; j < cols; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[rows - 1][cols - 1];
};
复杂度
- 时间:mn;
- 空间:mn;
最大正方形
题目
- 221;
思路
- 划分阶段:根据正方形右下角坐标进行划分;
- 定义状态:dp[i][j] 表示以 [i,j] 为右下角的最大正方形边长;
- 状态转移方程;
- 维护最大边长 res;
- 若 matrix[i][j] === 0,不可能为正方形,dp[i][j] = 0;
- 反之,dp[i][j] 由该位置的上方,左侧,左上方的最小值约束;
- 即 min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1]) + 1;
- 起始条件:首行首列,有 1 为 1,反之为 0;
- 终止条件:遍历矩阵,返回 res;
/**
* @param {character[][]} matrix
* @return {number}
*/
var maximalSquare = function (matrix) {
const rows = matrix.length;
const cols = matrix[0].length;
const dp = Array.from({ length: rows }, () => new Array(cols).fill(0));
let res = 0;
for (let i = 0; i < rows; i++) {
for (let j = 0; j < cols; j++) {
if (matrix[i][j] === "0") continue;
if (i === 0 || j === 0) dp[i][j] = 1;
else
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1;
res = Math.max(res, dp[i][j]);
}
}
return res * res;
};
复杂度
- 时间:mn;
- 空间:mn;
整数拆分
题目
- 343;
思路
- 划分阶段:根据正整数 n 划分 0 - n;
- 定义状态:dp[i] 为 n 划分后的最大乘积;
- 状态转移方程;
- 当 i >= 2,i 拆分的第一个正整数假设为 j (
1<=j<i); - 若只拆分两个整数,乘积为 j * (i-j);
- 反之,乘积为 j * dp[i-j];
- 遍历 j,dp[i] =
- 当 i >= 2,i 拆分的第一个正整数假设为 j (
- 初始条件,0 和 1 无法拆分,dp[0]=dp[1]=0;
- 终止条件:dp[n];
/**
* @param {number} n
* @return {number}
*/
var integerBreak = function (n) {
const dp = new Array(n + 1).fill(0);
for (let i = 2; i < n + 1; i++) {
for (let j = 1; j < i; j++) {
dp[i] = Math.max((i - j) * j, dp[i - j] * j, dp[i]);
}
}
return dp[n];
};
复杂度
- 时间:n^2;
- 空间:n;
乘积最大子数组
题目
- 152;
思路
- 划分阶段:根据数组元素划分;
- 定义状态:dp[i] 即以 nums[i] 结尾的乘积最大子数组;
- 状态转移方程;
- 由于数组存在负数,正数与负数相乘,会让最大乘积变最小乘积,反之依然,故维护数组最大值和最小值;
- dpMax[i]=max(dpMax[i-1]*nums[i-1],nums[i-1],dpMin[i-1]*nums[i-1]);
- dpMin[i]=min(dpMin[i-1]*nums[i-1],nums[i-1],dpMax[i-1]*nums[i-1]);
- 初始条件:dpMax[0]=dpMin[0]=nums[0];
- 终止条件:遍历数组,返回 dpMax[i];
/**
* @param {number[]} nums
* @return {number}
*/
var maxProduct = function (nums) {
const dpMax = new Array(nums.length);
const dpMin = new Array(nums.length);
dpMax[0] = dpMin[0] = nums[0];
for (let i = 1; i < nums.length; i++) {
dpMax[i] = Math.max(
dpMax[i - 1] * nums[i],
nums[i],
dpMin[i - 1] * nums[i]
);
dpMin[i] = Math.min(
dpMin[i - 1] * nums[i],
nums[i],
dpMax[i - 1] * nums[i]
);
}
return Math.max(...dpMax);
};
复杂度
- 时间:n;
- 空间:1;
打家劫舍 1
题目
- 198;
思路
- 划分阶段:根据房屋简述划分;
- 定义状态:dp[i] 表示前 i 间为止能偷窃的最高金额;
- 状态转移方程;
- 当偷窃第 i 间房屋时;
- 如果偷窃该房屋,则房屋 i-1 间无法偷窃,dp[i]=dp[i-2]+nums[i-1];
- 反之 dp[i]=dp[i-1];
- 初始状态:dp[0] = 0,dp[1]=nums[0];
- 终止条件:遍历数组,返回 dp[-1];
/**
* @param {number[]} nums
* @return {number}
*/
var rob = function (nums) {
const dp = new Array(nums.length + 1);
dp[0] = 0;
dp[1] = nums[0];
for (let i = 2; i < nums.length + 1; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]);
}
return dp[nums.length];
};
复杂度
- 时间:n;
- 空间:1;
打家劫舍 2
题目
- 213;
思路
- 偷第一间,就不能偷最后一件;
- 故将问题分解为两个子问题,无视第一间和无视最后一件;
- 即偷窃 [0,-2] 和 [1,-1] 范围内首尾不相连的房屋;
- 转变为 2 个打家劫舍 1;
/**
* @param {number[]} nums
* @return {number}
*/
var rob = function (nums) {
const helper = (nums) => {
const dp = new Array(nums.length + 1);
dp[0] = 0;
dp[1] = nums[0];
for (let i = 2; i < nums.length + 1; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]);
}
return dp[nums.length];
};
if (nums.length === 1) return nums[0];
const v1 = helper(nums.slice(1));
const v2 = helper(nums.slice(0, -1));
return Math.max(v1, v2);
};
复杂度
- 时间:n;
- 空间:n;
解码方法
题目
- 091;
思路
- 划分阶段:根据前 i 个字符串划分;
- 定义状态:dp[i] 表示前 i 个字符串可能构成的方案数;
- 状态转移方程;
- 使用一个字符:
dp[i] = dp[i] + dp[i-1] (s[i-1]!=0); - 使用两个字符:
dp[i] = dp[i] + dp[i-2] (s[i-2]!=0, s[i-2:i-1]<=26);
- 使用一个字符:
- 起始条件:dp[0]=1,其余为 0;
- 终止条件:遍历数组,返回 dp[n];
/**
* @param {string} s
* @return {number}
*/
var numDecodings = function (s) {
const n = s.length;
const dp = new Array(s.length + 1).fill(0);
dp[0] = 1;
for (let i = 1; i <= n; i++) {
if (s[i - 1] !== "0") dp[i] += dp[i - 1];
if (i > 1 && s[i - 2] !== "0" && Number(s.slice(i - 2, i)) <= 26)
dp[i] += dp[i - 2];
}
return dp[n];
};
复杂度
- 时间:n;
- 空间:n;
正则表达式匹配
题目
- 10;
思路
- 划分阶段:根据 s 和 p 前 i 个字符串划分;
- 定义状态:dp[i][j] 表示 s 的前 i 个字符与 p 的前 j 个字符是否匹配;
- 状态转移方程;
- 如果 s[i-1]===p[j-1] 或者 p[j-1] = 。,说明对应字符匹配,dp[i][j]=dp[i-1][j-1];
- 如果 p[j-1]=*,对 p 的第 j -1 个字符进行若干次匹配;
- 如果 s[i-1]!==p[j-2] 且 p[j-2] != 。,说明第 i 个字符和第 j-1 个字符无法匹配;
- dp[i][j]=dp[i][j-2];
- 反之匹配;
- 0 个:dp[i][j]=dp[i][j-2];
- 1 个:dp[i][j]=dp[i-1][j-2];
- 2 个:dp[i][k]=dp[i-2][j-2];
- 。。。
- 1 - n 个优化公式:dp[i][j]=dp[i-1][j],直接死记硬背吧;
- 如果 s[i-1]!==p[j-2] 且 p[j-2] != 。,说明第 i 个字符和第 j-1 个字符无法匹配;
- 起始条件;
- dp[0][0]=true,其余为 false;
- p[j-1]="*",取决于 j-2 是否也为 *,即 dp[0][j]=dp[0][j-2];
- 终止条件:遍历数组,返回 dp[m][n];
/**
* @param {string} s
* @param {string} p
* @return {boolean}
*/
var isMatch = function (s, p) {
const m = s.length;
const n = p.length;
const dp = Array.from(
{
length: m + 1,
},
() => new Array(n + 1).fill(false)
);
dp[0][0] = true;
for (let i = 1; i <= n; i++) {
if (p[i - 1] === "*") dp[0][i] = dp[0][i - 2];
}
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (s[i - 1] === p[j - 1] || p[j - 1] === ".")
dp[i][j] = dp[i - 1][j - 1];
else if (p[j - 1] === "*")
if (s[i - 1] !== p[j - 2] && p[j - 2] !== ".") dp[i][j] = dp[i][j - 2];
else dp[i][j] = dp[i][j - 2] || dp[i - 1][j];
}
}
return dp[m][n];
};
复杂度
- 时间:mn;
- 空间:mn;
通配符匹配
题目
- 44;
思路
- 思路类似于正则表达式匹配;
- 划分阶段:根据 s 和 p 前 i 个字符串划分;
- 定义状态:dp[i][j] 表示 s 的前 i 个字符与 p 的前 j 个字符是否匹配;
- 状态转移方程;
- 如果 s[i-1]===p[j-1] 或者 p[j-1] = ?,说明对应字符匹配,dp[i][j]=dp[i-1][j-1];
- 如果 p[j-1]=*,则 p[j-1] 匹配 s 任意数量字符;
- 0 个:dp[i][j]=dp[i][j-1];
- 1 个:dp[i][j]=dp[i-1][j-1];
- 2 个:dp[i][k]=dp[i-2][j-1];
- 。。。
- 1 - n 个优化公式:dp[i][j]=dp[i-1][j],直接死记硬背吧;
- 起始条件;
- dp[0][0]=true,其余为 false;
- s 为空,p 以若干个 * 前导,dp[0][j]=true;
- 终止条件:遍历数组,返回 dp[m][n];
/**
* @param {string} s
* @param {string} p
* @return {boolean}
*/
var isMatch = function (s, p) {
const m = s.length;
const n = p.length;
const dp = Array.from(
{
length: s.length + 1,
},
() => new Array(p.length + 1).fill(false)
);
dp[0][0] = true;
for (let i = 1; i <= n; i++) {
if (p[i - 1] !== "*") break;
dp[0][i] = true;
}
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (s[i - 1] === p[j - 1] || p[j - 1] === "?")
dp[i][j] = dp[i - 1][j - 1];
else if (p[j - 1] === "*") dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
}
}
return dp[m][n];
};
复杂度
- 时间:mn;
- 空间:mn;
跳跃游戏 1
题目
- 55;
思路
- 划分阶段:根据数组索引划分;
- 定义状态:dp[i] 表示从位置 0 出发,到达位置 i,可以跳出的最大距离;
- 状态转移公式;
- 如果经过 [0,i-1],可以到达 i:dp[i-1]>=i,则 dp[i]=max(dp[i-1],i+nums[i]);
- 反之 dp[i-1] < i,则 dp[i]=dp[i-1];
- 初始条件:dp[0]=nums[0];
- 终止条件:返回 dp[n-1];
/**
* @param {number[]} nums
* @return {boolean}
*/
var canJump = function (nums) {
const n = nums.length;
const dp = new Array(n).fill(0);
dp[0] = nums[0];
for (let i = 1; i < n; i++) {
if (dp[i - 1] >= i) dp[i] = Math.max(dp[i - 1], nums[i] + i);
else dp[i] = dp[i - 1];
}
return dp[n - 1] >= n - 1;
};
复杂度
- 时间:n;
- 空间:n;
跳跃游戏 2
题目
- 45;
思路
- 划分阶段:根据数组索引划分;
- 定义状态:dp[i] 表示从位置 0 出发,到达位置 i,需要的最少步骤;
- 状态转移公式;
- 对于位置 i,如果可以从位置 j 调到;
- j+nums[j]>=i;
- dp[i]=min[dp[i],dp[j]+1];
- 遍历位置 j;
- 对于位置 i,如果可以从位置 j 调到;
- 初始条件:dp[i]=Infinity;
- 终止条件:返回 dp[n-1];
/**
* @param {number[]} nums
* @return {number}
*/
var jump = function (nums) {
const n = nums.length;
const dp = new Array(n).fill(Infinity);
dp[0] = 0;
for (let i = 0; i < n; i++) {
for (let j = 0; j < i; j++) {
if (j + nums[j] >= i) dp[i] = Math.min(dp[i], dp[j] + 1);
}
}
return dp[n - 1];
};
复杂度
- 时间:n^2;
- 空间:n;
单词拆分
题目
- 139;
思路
- 划分阶段:根据前 i 个字符划分;
- 定义状态:dp[i] 表示 s[0:i] 是否能拆分为单词;
- 状态转移方程;
- 遍历 j (
1<=j<i); - s[j-1:i] 在字典中,dp[i]=dp[j-1];
- j-1 是第 j 个,所以 j 前面的 dp 为 dp[j-1];
- 反之 dp[i]=false;
- 遍历 j (
- 起始条件:dp[0]=true,其余为 false;
- 终止条件:返回 dp[n];
/**
* @param {string} s
* @param {string[]} wordDict
* @return {boolean}
*/
var wordBreak = function (s, wordDict) {
const n = s.length;
const dp = new Array(n + 1).fill(false);
dp[0] = true;
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= i; j++) {
if (dp[i] === true) break;
const str = s.slice(j - 1, i);
if (wordDict.includes(str)) dp[i] = dp[j - 1];
}
}
return dp[n];
};
复杂度
- 时间:n^2;
- 空间:n;
三角形最小路径和
题目
- 120;
思路
- 划分阶段:根据行数和列数划分;
- 定义状态:dp[i][j] 表示移动至第 i 行,第 j 列的最小路径和;
- 状态转移方程;
- 上一步行数为 i-1 行,列数为 j-1 列或 j 列;
- dp[i][j]=min(dp[i-1][j-1],dp[i-1][j])+triangle[i-1][j-1]
- 起始条件:dp[1][1]=triangle[0][0];
- 终止条件:返回 min(dp[i]);
/**
* @param {number[][]} triangle
* @return {number}
*/
var minimumTotal = function (triangle) {
const n = triangle.length;
const dp = Array.from(
{
length: n + 1,
},
() => new Array(n + 1).fill(Infinity)
);
dp[1][1] = triangle[0][0];
for (let i = 2; i <= n; i++) {
for (let j = 1; j <= i; j++) {
dp[i][j] =
Math.min(dp[i - 1][j], dp[i - 1][j - 1]) + triangle[i - 1][j - 1];
}
}
return Math.min(...dp[n]);
};
复杂度
- 时间:n^2;
- 空间:n^2;
鸡蛋掉落
题目
- 887;
思路
- 逆向思路;
- 已知 k 个鸡蛋,最多扔 x 次,求最多可以检测多少层;
- 划分阶段:根据鸡蛋个数和扔鸡蛋次数划分;
- 定义状态:dp[i][j] 表示一共 i 个鸡蛋,最多扔 j 次,最多可以监测的楼层个数;
- 因为一共 n 层楼,所以 j 最多是 n;
- 状态转移方程;
- 在 1 - n 层任意一层 x 扔鸡蛋;
- 如果鸡蛋没碎,i=i,j=j-1,最多可以检查 dp[i][j-1] 层楼层;
- 如果碎了,i=i-1,j=j-1,最多可以检查 dp[i-1][j-1] 层楼层;
- 加上第 x 层,dp[i][j]=dp[i][j-1]+dp[i-1][j-1]+1;
- 初始条件:dp=0;
- 终止条件:k 个鸡蛋全部使用且 dp[i][j] >= n,返回最小的 j;
/**
* @param {number} k
* @param {number} n
* @return {number}
*/
var superEggDrop = function (k, n) {
const dp = Array.from(
{
length: k + 1,
},
() => new Array(n + 1).fill(0)
);
for (let i = 1; i <= k; i++) {
for (let j = 1; j <= n; j++) {
dp[i][j] = dp[i][j - 1] + dp[i - 1][j - 1] + 1;
if (i === k && dp[i][j] >= n) return j;
}
}
return n;
};
复杂度
- 时间:nk;
- 空间:nk;
交错字符串
题目
- 97;
思路
- 划分阶段:根据 s1 的前 i 个字符和 s2 的前 j 个字符划分;
- 定义状态:dp[i][j] 为 s1 的前 i 个字符和 s2 的前 j 个字符能否组成 s3 的前 i+j 个字符;
- 状态转移方程;
- 若 s3 最后一个字符为 i:dp[i][j]=dp[i-1][j];
- 反之:dp[i][j]=dp[i][j-1];
- 起始条件;
- dp[0][0]=true;
- 若 s1 或 s2 为空,遍历 s1/s2,其余 s3 相同的子字符串对应 dp 为 true;
- 终止条件:返回 dp[m][n];
/**
* @param {string} s1
* @param {string} s2
* @param {string} s3
* @return {boolean}
*/
var isInterleave = function (s1, s2, s3) {
const m = s1.length;
const n = s2.length;
if (m + n !== s3.length) return false;
const dp = Array.from(
{
length: m + 1,
},
() => new Array(n + 1).fill(false)
);
dp[0][0] = true;
for (let i = 1; i <= m; i++) {
if (s1[i - 1] !== s3[i - 1]) break;
dp[i][0] = true;
}
for (let i = 1; i <= n; i++) {
if (s2[i - 1] !== s3[i - 1]) break;
dp[0][i] = true;
}
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (s1[i - 1] === s3[i + j - 1]) dp[i][j] = dp[i - 1][j];
if (s2[j - 1] === s3[i + j - 1]) dp[i][j] = dp[i][j] || dp[i][j - 1];
}
}
return dp[m][n];
};
复杂度
- 时间:n^2;
- 空间:n^2;
买卖股票的最佳时机 3
题目
- 123;
思路
- 划分阶段:根据索引和持有股票状态划分;
- 定义状态:dp[i][j] 表示 [0,i]区间,不同持有股票的状态,所获得的最大价值;
- 四种股票状态:不进行任何操作 + 第一次持有股票 + 第一次不持有股票 + 第二次持有股票 + 第二次不持有股票;
- 状态转移方程;
- dp[i][0]:dp[i][0]=dp[i-1][0];
- dp[i][1]:具有第一次持有股票的状态;
- 不操作:dp[i][1]=dp[i-1][1];
- 买入股票:dp[i][1]=dp[i-1][0]-prices[i];
- 选取两者最大值;
- dp[i][2]:具有第一次未持有股票状态;
- 不操作:dp[i][2]=dp[i-1][2];
- 卖出股票:dp[i][1]=dp[i-1][1]+prices[i];
- 选取两者最大值;
- 3 和 4 状态同理;
- 初始条件:dp[0][0/2/4] = 0,dp[0][1/3]=-prices[0];
- 终止条件:返回 dp[n][4];
/**
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function (prices) {
const n = prices.length;
const dp = Array.from(
{
length: n,
},
() => new Array(5).fill(0)
);
dp[0][1] = dp[0][3] = -prices[0];
for (let i = 1; i < n; i++) {
dp[i][0] = dp[i - 1][0];
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return Math.max(...dp[n - 1]);
};
复杂度
- 时间:n;
- 空间:n^2;
背包问题
0-1 背包
问题概述
- 给定 n 个物品,重量为 cap 的背包;
- 物品重量为
wgt[i],价值为val[i]; - 每个物品只能选择一次;
- 求背包能够放入物品的最大值;
基本思路
- 划分状态:根据物品序号和当前背包重量划分;
- 定义状态:dp[i][c] 为前 i 件物品放入一个 c 重量的背包,可获得的最大价值;
- 状态转移方程;
- 只考虑第 i 件物品,只有放入和不放入两个选项;
- 不放入物品,dp[i][c] = dp[i-1][c];
- 放入物品,dp[i][c] = dp[i-1][c-wgt[i-1]] + val[i-1];
- i - 1 即前 i - 1 件物品;
- c - wgt[i-1] 即去除第 i 件物品重量;
- val[i-1] 即第 i 件物品价值;
- 根据背包重量上限判断第 i 件物品能否放入;
- 只考虑第 i 件物品,只有放入和不放入两个选项;
- 初始条件:无物品或背包为 0,价值为 0,即 dp[i][0] 和 dp[0][i] 为 0;
- 终止条件:遍历到 dp 表末端,返回 dp[n][c];
/* 0-1 背包: 动态规划 */
function knapsackDP(wgt, val, cap) {
const n = wgt.length;
// 初始化 dp 表
const dp = Array(n + 1)
.fill(0)
.map(() => Array(cap + 1).fill(0));
// 状态转移
for (let i = 1; i <= n; i++) {
for (let c = 0; c <= cap; c++) {
if (wgt[i - 1] > c) {
// 若超过背包重量, 则不选物品 i
dp[i][c] = dp[i - 1][c];
} else {
// 不选和选物品 i 这两种方案的较大值
dp[i][c] = Math.max(
dp[i - 1][c],
dp[i - 1][c - wgt[i - 1]] + val[i - 1]
);
}
}
}
return dp[n][cap];
}
滚动数组优化
- 每个状态只和左上方和上方状态和有关,即只和 dp 表当前行和上一行有关 (第 i 件物品和 i - 1 物品);
- 只使用一个一维数组保存上一状态和当前状态 (背包重量);
- 使用倒序方式遍历更新一维数组;
- 上方状态:不会改变,不用考虑;
- 左上方状态:倒序遍历避免当前状态覆盖上一状态;
function knapsackDPComp(wgt, val, cap) {
const n = wgt.length;
const dp = Array(cap + 1).fill(0);
for (let i = 1; i <= n; i++) {
// 倒序遍历
for (let c = cap; c >= 0; c--) {
if (wgt[i - 1] <= c) {
dp[c] = Math.max(dp[c], dp[c - wgt[i - 1]] + val[i - 1]);
}
}
}
return dp[cap];
}
完全背包
问题概述
- 给定 n 个物品,重量为 cap 的背包;
- 物品重量为
wgt[i],价值为val[i]; - 每个物品数量没有限制;
- 求背包能够放入物品的最大值;
基本思路
- 状态转移方程;
- 只考虑第 i 件物品,只有放入和不放入两个选项;
- 不放入物品,dp[i][c] = dp[i-1][c];
- 放入物品,dp[i][c] = dp[i][c-wgt[i-1]] + val[i-1];
- i 即前 i 件物品,因为完全背包没有物品限制;
- c - wgt[i-1] 即去除第 i 件物品重量;
- val[i-1] 即第 i 件物品价值;
- 根据背包重量上限判断第 i 件物品能否放入;
- 只考虑第 i 件物品,只有放入和不放入两个选项;
/* 完全背包: 动态规划 */
function unboundedKnapsackDP(wgt, val, cap) {
const n = wgt.length;
// 初始化 dp 表
const dp = Array.from({ length: n + 1 }, () =>
Array.from({ length: cap + 1 }, () => 0)
);
// 状态转移
for (let i = 1; i <= n; i++) {
for (let c = 0; c <= cap; c++) {
if (wgt[i - 1] > c) {
// 若超过背包重量, 则不选物品 i
dp[i][c] = dp[i - 1][c];
} else {
// 不选和选物品 i 这两种方案的较大值
dp[i][c] = Math.max(dp[i - 1][c], dp[i][c - wgt[i - 1]] + val[i - 1]);
}
}
}
return dp[n][cap];
}
空间优化
- 每个状态只和左方状态和上方有关,即只和 dp 表当前行和上一行有关 (第 i 件物品和 i - 1 物品);
- 只使用一个一维数组保存上一状态和当前状态 (背包重量);
- 使用正序方式遍历更新一维数组;
- 上方状态:不会改变,不用考虑;
- 左方状态:正序遍历,保证左方状态的更新;
/* 完全背包: 空间优化后的动态规划 */
function unboundedKnapsackDPComp(wgt, val, cap) {
const n = wgt.length;
// 初始化 dp 表
const dp = Array.from({ length: cap + 1 }, () => 0);
// 状态转移
for (let i = 1; i <= n; i++) {
for (let c = 0; c <= cap; c++) {
if (wgt[i - 1] <= c) {
// 不选和选物品 i 这两种方案的较大值
dp[c] = Math.max(dp[c], dp[c - wgt[i - 1]] + val[i - 1]);
}
}
}
return dp[cap];
}
多重背包
问题概述
- 给定 n 个物品,重量为 cap 的背包;
- 物品重量为
wgt[i],价值为val[i],件数为count[i]; - 求背包能够放入物品的最大值;
基本思路
- 01 背包转换;
- 对于第 i 件物品,可以最多选择 count[i] 次;
- 从 0 - count[i] 进行遍历,转换为 01 背包问题;
- 划分状态:根据物品序号和当前背包重量划分;
- 定义状态:dp[i][c] 为前 i 件物品放入一个 c 重量的背包,可获得的最大价值;
- 状态转移方程;
- 只考虑第 i 件物品,只有放入和不放入两个选项;
- 不放入物品,dp[i][c] = dp[i-1][c];
- 放入物品 k 次,dp[i][c] = dp[i][c-k*wgt[i-1]] + k*val[i-1];
- i 即前 i 件物品,因为完全背包没有物品限制;
- c - k*wgt[i-1] 即去除第 i 件物品重量;
- k*val[i-1] 即第 i 件物品价值;
- 根据背包重量上限判断 k 个第 i 件物品能否放入;
- 只考虑第 i 件物品,只有放入和不放入两个选项;
- 初始条件:无物品或背包为 0,价值为 0,即 dp[i][0] 和 dp[0][i] 为 0;
- 终止条件:遍历到 dp 表末端,返回 dp[n][c];
/* 多重背包: 动态规划 */
function unboundedKnapsackDP(wgt, val, cap, count) {
const n = wgt.length;
// 初始化 dp 表
const dp = Array.from({ length: n + 1 }, () =>
Array.from({ length: cap + 1 }, () => 0)
);
// 状态转移
for (let i = 1; i <= n; i++) {
for (let c = 0; c <= cap; c++) {
for (let k = 0; k <= Math.min(count[i - 1]); k++) {
if (k * wgt[i - 1] > c) {
// 若超过背包重量, 则不选物品 i
dp[i][c] = dp[i - 1][c];
} else {
// 不选和选物品 i 这两种方案的较大值
dp[i][c] = Math.max(
dp[i - 1][c],
dp[i - 1][c - k * wgt[i - 1]] + k * val[i - 1]
);
}
}
}
}
return dp[n][cap];
}
空间优化
- 参考 01 背包;
分组背包
问题概述
- 01 背包变种;
- 给定 n 组物品,重量为 cap 的背包;
- 第 i 组物品件数为
groupCount[i],第 n 组第 i 个物品重量为wgt[i][j],价值为val[i][j]; - 每组物品只能选择一个;
- 求背包能够放入物品的最大值;
基本思路
- 划分状态:根据物品组数和当前背包重量划分;
- 定义状态:dp[i][c] 为前 i 组物品放入一个 c 重量的背包,可获得的最大价值;
- 状态转移方程;
- 只考虑第 i 组物品,只有放入和不放入两个选项;
- 不放入该组物品,dp[i][c] = dp[i-1][c];
- 放入该组第 j 个物品,dp[i][c] = dp[i-1][c-wgt[i-1][j]] + val[i-1][j];
- i - 1 即前 i - 1 件物品;
- c - wgt[i-1][j] 即去除第 i 件物品重量;
- val[i-1][j] 即第 i 件物品价值;
- 根据背包重量上限判断 k 个第 i 件物品能否放入;
- 只考虑第 i 组物品,只有放入和不放入两个选项;
- 初始条件:无物品或背包为 0,价值为 0,即 dp[i][0] 和 dp[0][i] 为 0;
- 终止条件:遍历到 dp 表末端,返回 dp[n][c];
/* 0-1 背包: 动态规划 */
function knapsackDP(wgt, val, cap, groupCount) {
const n = wgt.length;
// 初始化 dp 表
const dp = Array(n + 1)
.fill(0)
.map(() => Array(cap + 1).fill(0));
// 状态转移
for (let i = 1; i <= n; i++) {
for (let c = 0; c <= cap; c++) {
for (let j = 0; i < groupCount[i - 1]; j++) {
if (wgt[i - 1][j] > c) {
// 若超过背包重量, 则不选物品 i
dp[i][c] = dp[i - 1][c];
} else {
// 不选和选物品 i 这两种方案的较大值
dp[i][c] = Math.max(
dp[i - 1][c],
dp[i - 1][c - wgt[i - 1][j]] + val[i - 1][j]
);
}
}
}
}
return dp[n][cap];
}
空间优化
- 同 01 背包;
二维背包问题
问题概述
- 给定 n 个物品,重量为 cap 的背包,容量为 v;
- 物品重量为
wgt[i],价值为val[i],容量为vol[i]; - 每个物品只能选择一次;
- 求背包能够放入物品的最大值;
基本思路
- 划分状态:根据物品序号和当前背包重量划分;
- 定义状态:dp[i][c][v] 为前 i 件物品放入一个 c 重量,v 容量的背包,可获得的最大价值;
- 状态转移方程;
- 只考虑第 i 件物品,只有放入和不放入两个选项;
- 不放入物品,dp[i][c][v] = dp[i-1][c][v];
- 放入物品,dp[i][c] = dp[i-1][c-wgt[i-1]][v-volume[i-1] + val[i-1];
- i - 1 即前 i - 1 件物品;
- c - wgt[i-1] 即去除第 i 件物品重量;
- v - vol[i-1] 即去除第 i 件物品容量;
- val[i-1] 即第 i 件物品价值;
- 根据背包重量上限和容量上限判断第 i 件物品能否放入;
- 只考虑第 i 件物品,只有放入和不放入两个选项;
- 初始条件:无物品,背包重量为 0,背包容量为 0,价值为 0,即 dp[i][0][0],dp[0][i][0] 和 dp[0][0][i] 为 0;
- 终止条件:遍历到 dp 表末端,返回 dp[n][c][v];
/* 0-1 背包: 动态规划 */
function knapsackDP(wgt, val, vol, cap, v) {
const n = wgt.length;
// 初始化 dp 表
const dp = Array(n + 1)
.fill(0)
.map(() =>
Array(cap + 1)
.fill(0)
.map(() => Array(v + 1).fill(0))
);
// 状态转移
for (let i = 1; i <= n; i++) {
for (let c = 0; c <= cap; c++) {
for (let v = 0; v <= vol; v++) {
if (wgt[i - 1] > c || vol[i - 1] > v) {
// 若超过背包重量, 则不选物品 i
dp[i][c][v] = dp[i - 1][c][b];
} else {
// 不选和选物品 i 这两种方案的较大值
dp[i][c][v] = Math.max(
dp[i - 1][c][v],
dp[i - 1][c - wgt[i - 1]][v - vol[i - 1]] + val[i - 1]
);
}
}
}
}
return dp[n][cap][v];
}
滚动数组优化
- 参考 01 背包;
混合背包
问题概述
- 给定 n 个物品,重量为 cap 的背包;
- 物品重量为
wgt[i],价值为val[i],件数为count[i];- 0:无穷件;
- i:i 件;
- 求背包能够放入物品的最大值;
基本思路
- 01 背包,完全背包和多重背包的混合;
- 根据 count 的不同分别使用不同背包的解决方法;
/* 多重背包: 动态规划 */
function unboundedKnapsackDP(wgt, val, cap, count) {
const n = wgt.length;
// 初始化 dp 表
const dp = Array.from({ length: n + 1 }, () =>
Array.from({ length: cap + 1 }, () => 0)
);
// 状态转移
for (let i = 1; i <= n; i++) {
if (count[i - 1] === 1) {
// 01 背包
} else if (count[i - 1] === 0) {
// 无穷背包
} else {
// 多重背包
}
}
return dp[n][cap];
}
背包问题变种
背包问题第二层循环 0 和 1
- 第二层循环是否以 0 或 1 为起点/终点;
- 关键在于
dp[0][i] (i!=0)是否恒定不变;- 大部分最值问题和存在问题,恒定不变,所以 1 即可;
- 但是组合问题,可能发生变化,所以需要 0;
最值问题
问题概述
- 背包问题变种;
- 求各种最大值,最小值;
基本思路
- 背包问题默认 dp;
- 状态转移方程;
- 01 背包:dp[i][c] = Math.max(dp[i - 1][c],dp[i-1]c - wgt[i - 1]] + value);
- 完全背包:dp[i][c] = Math.max(dp[i - 1][c],dp[i]c - wgt[i - 1]] + value);
- value;
- 物品价值:val[i - 1];
- 常数:1;
- 。。。;
组合问题
问题概述
- 背包问题变种;
- 求总重量不超过重量上限的情况下,可以选择的方案数/组合;
基本思路
- 状态转移方程;
- 只考虑第 i 件物品,根据背包重量上限判断第 i 件物品能否放入;
- 无法放入物品物品,dp[i][c] = dp[i-1][c];
- 可以放入物品,有不放入和放入两个选择,将背包问题的求最大值改为相加;
- 01 背包:dp[i][c] = dp[i-1][c] + dp[i-1][c-wgt[i-1]];
- 完全背包 dp[i][c] = dp[i-1][c] + dp[i][c-wgt[i-1]];
- 只考虑第 i 件物品,根据背包重量上限判断第 i 件物品能否放入;
- 初始条件:dp[i][0] 或 dp[0][i] = 1,其余为 0,根据具体问题分析;
是否存在问题
问题概述
- 背包问题变种;
- 背包是否存在某个物品组合,满足某个特定条件;
基本思路
- 状态转移方程;
- 只考虑第 i 件物品,根据背包重量上限判断第 i 件物品能否放入;
- 无法放入物品物品,dp[i][c] = dp[i-1][c];
- 可以放入物品,判断上一状态是否存在;
- 01 背包:dp[i][c] = dp[i-1][c] || dp[i-1][c-wgt[i-1]];
- 完全背包 dp[i][c] = dp[i-1][c] || dp[i][c-wgt[i-1]];
- 只考虑第 i 件物品,根据背包重量上限判断第 i 件物品能否放入;
- 初始条件:dp[i][0] 或 dp[0][i] = true,其余状态默认为 false,根据具体问题分析;
求恰好装满背包
问题概述
- 背包问题变种;
- 求背包恰好装满的最值/组合数量/方案数;
基本思路
- 涉及初始条件和终止条件的变化;
- 初始条件;
- 最值问题;
- 背包上限为 0,必然装满背包,即 dp[i][0] = 0;
- 其余初始状态假设都不能放入背包,定义为 -Infinity/Infinity;
- 组合问题;
- 背包上限为 0,必然装满背包,即 dp[i][0] = 1;
- 其余初始状态假设方案均为 0;
- 存在问题;
- 背包上限为 0,必然装满背包,即 dp[i][0] = true;
- 其余初始状态假设方案均为 false;
- 最值问题;
- 终止条件:遍历到 dp 表末端,根据具体问题,返回 dp[n][c];
- 最值问题:判断 dp[n][c] 是否等于 -Infinity/Infinity,根据问题返回对应值;
- 其余问题:直接返回;
背包问题题目
分割等和子集
题目
- 416;
思路
- 转换问题描述,即从数组选择一些元素,使子集和恰好等于整个数组元素和的一般;
- 转换为 01 背包问题;
- nums 代表物品价值,nums 总和的一半代表背包特定价值;
- 判断背包是否存在若干物品组合,使得背包价值等于特定值;
- 状态转移方程:01 背包 + 存在问题;
- 物品数量 nums.length;
- 物品价值:nums[i];
/**
* @param {number[]} nums
* @return {boolean}
*/
var canPartition = function (nums) {
const sum = nums.reduce((a, b) => a + b, 0);
if (sum % 2 === 1) return false;
const n = nums.length;
const cap = sum / 2;
const dp = Array.from(
{
length: n + 1,
},
() => new Array(cap + 1).fill(false)
);
for (let i = 0; i <= n; i++) {
dp[i][0] = true;
}
for (let i = 1; i <= n; i++) {
for (let j = 0; j <= cap; j++) {
if (nums[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];
}
}
}
return dp[n][cap];
};
复杂度
- 时间:n * target;
- 空间:target;
目标和
题目
- 494;
思路
- 问题分析;
- 数组所有元素和为 sum,添加正号的和为 x,添加负号的和为 s,x + s = sum;
- 又因为 x-s = target,x = (sum+target)/2;
- 又因为 x 必然是整数,所以 sum+target 必然是偶数,且 target 必然小于 sum;
- 转换为 01 背包问题;
- nums 代表物品价值,x 代表背包特定价值;
- 计算 nums 若干物品组合的方案,使得背包价值等于特定值;
- 状态转移方程:01 背包 + 组合问题;
- 物品数量 nums.length;
- 物品价值/重量:nums[i];
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var findTargetSumWays = function (nums, target) {
const sum = nums.reduce((a, b) => a + b, 0);
const temp = sum + target;
if (temp % 2 === 1 || temp < 0) return 0;
const W = temp / 2;
const n = nums.length;
const value = nums;
const weight = nums;
const dp = Array.from(
{
length: n + 1,
},
() => new Array(W + 1).fill(0)
);
for (let i = 0; i <= n; i++) {
dp[i][0] = 1;
}
for (let i = 1; i <= n; i++) {
for (let j = 0; j <= W; j++) {
if (weight[i - 1] > j) dp[i][j] = dp[i - 1][j];
else dp[i][j] = dp[i - 1][j] + dp[i - 1][j - weight[i - 1]];
}
}
return dp[n][W];
};
复杂度
- 时间:2^n;
- 空间:n;
零钱兑换 1
题目
- 322;
思路
- 转换为完全背包问题;
- 即 n 种不同硬币,每种硬币无线选取,恰好凑成指定金额,求最少硬币数量;
- 完全背包问题 + 恰好装满背包
- 状态转移方程:完全背包;
- 初始条件:恰好装满背包;
/**
* @param {number[]} coins
* @param {number} amount
* @return {number}
*/
var coinChange = function (coins, amount) {
const n = coins.length;
const value = coins;
const dp = Array.from(
{
length: n + 1,
},
() => new Array(amount + 1).fill(Infinity)
);
for (let i = 0; i <= n; i++) {
dp[i][0] = 0;
}
for (let i = 1; i <= n; i++) {
for (let j = 0; j <= amount; j++) {
if (value[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - value[i - 1]] + 1);
}
}
}
return dp[n][amount] === Infinity ? -1 : dp[n][amount];
};
复杂度
- 时间:amount * size;
- 空间:amount * size;
零钱兑换 2
题目
- 518;
思路
- 转换为完全背包问题;
- 即 n 种不同硬币,每种硬币无线选取,恰好凑成指定金额,求组合方案数;
- 完全背包问题 + 刚好凑满 + 组合问题
- 状态转移方程:完全背包 + 组合问题;
- 相加 + 第二层循环从 0 开始;
- 初始条件:组合问题 + 刚好凑满;
- dp[0][0] = 1,其余为 Infinity
/**
* @param {number} amount
* @param {number[]} coins
* @return {number}
*/
var change = function (amount, coins) {
const n = coins.length;
const value = coins;
const dp = Array.from(
{
length: n + 1,
},
() => new Array(amount + 1).fill(0)
);
for (let i = 0; i <= n; i++) {
dp[i][0] = 1;
}
for (let i = 1; i <= n; i++) {
for (let j = 0; j <= amount; j++) {
if (value[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = dp[i - 1][j] + dp[i][j - value[i - 1]];
}
}
}
return dp[n][amount];
};
复杂度
- 时间:amount * size;
- 空间:amount * size;
区间 dp
区间动态规划
- 通过区间长度划分状态,使用区间左右索引作为状态维度;
- 一个状态由一个区间长度更小的状态转移;
- 通过小区间的最优解,进行合并,得到大区间的最优解;
常见分类
- 单个区间从中间向两侧转移:
[i+1,j-1]===>[i,j]; - 多个区间合并,转移至大区间;
[i,k] + [k,j]===>[i,j];
基本思路
从中间向两侧
- 状态转移方程:
dp[i][j]=max(dp[i+1][j-1], dp[i+1][j], dp[i][j-1]) + cost[i][j];- 由于使用下方,左方和左下方状态;
- i 倒序遍历,j 正序遍历;
- 根据具体题目处理
j>=i 或 j>i;- 默认区
i>=j,再判断 i===j 的特殊情况;
- 默认区
- 解题思路;
- 枚举区间起点;
- 枚举区间终点;
- 定义状态转移方程;
for i in range(size - 1, -1, -1):
for j in range(i+1, size):
dp[i][j] = max(dp[i + 1][j - 1], dp[i + 1][j], dp[i][j - 1]) + cost[i][j]
多个区间合并
- 状态转移方程:
dp[i][j]=max(dp[i][j], dp[i][k],dp[k][j] + cost[i][j]) (i<=k<=j); - 根据具体题目,考虑 k 的开闭区间;
- 解题思路;
- 枚举区间长度;
- 枚举区间起点,根据区间长度得到区间终点;
- 枚举区间分割点;
- 定义状态转移方程;
for l in range(1, n+1):
for i in range(n):
j = i + l - 1
if j >= n:
break
dp[i][j] = float('-inf')
for k in range(i+1, j):
dp[i][j] = max(dp[i][j], dp[i][k] + dp[k][j] + cost[i][j])
区间 dp 题目
最长回文子序列
题目
- 516;
思路
- 划分阶段:根据区间两端索引划分;
- 定义状态:dp[i][j] 表示 [i,j] 区间内的最长回文子序列长度;
- 状态转移方程;
- 如果
s[i] === s[j];- 如果 i===j,
dp[i][j]=1 - 反之
dp[i][j] = dp[i+1][j-1]+2
- 如果 i===j,
- 反之
dp[i][j]=max(dp[i][j-1], dp[i+1][j]);
- 如果
- 初始条件:全部为 0;
- 终止条件:返回 dp[0][size-1];
/**
* @param {string} s
* @return {number}
*/
var longestPalindromeSubseq = function (s) {
const size = s.length;
const dp = Array.from(
{
length: size,
},
() => new Array(size).fill(0)
);
for (let i = size - 1; i >= 0; i--) {
for (let j = i; j < size; j++) {
if (s[i] === s[j] || i === j) {
if (i === j) dp[i][j] = 1;
else dp[i][j] = dp[i + 1][j - 1] + 2;
} else dp[i][j] = Math.max(dp[i][j], dp[i + 1][j], dp[i][j - 1]);
}
}
return dp[0][size - 1];
};
复杂度
- 时间:n^2;
- 空间:n^2;
最长回文子串
题目
- 5;
思路
- 划分阶段:根据区间两端索引划分;
- 定义状态:
dp[i][j]表示s[i,j]区间是否为回文子串; - 状态转移方程;
- 维护最长子串长度和起始位置 len 和 start;
- 如果
s[i] === s[j];- 如果 j===i,
dp[i][j] = true; - 如果 j===i+1,
dp[i][j] = true; - 反之
dp[i][j] = dp[i+1][j-1];
- 如果 j===i,
- 反之
dp[i][j]=false;
- 初始条件:
dp[i][i]= true,其余为 false; - 终止条件:返回 s.slice(start,start+len);
/**
* @param {string} s
* @return {string}
*/
var longestPalindrome = function (s) {
const n = s.length;
const dp = Array.from({ length: n }, () => new Array(n).fill(false));
let start = 0;
let len = -1;
for (let i = n - 1; i >= 0; i--) {
for (let j = i; j < n; j++) {
if (s[i] !== s[j]) continue;
if (i === j || i + 1 === j) dp[i][j] = true;
else dp[i][j] = dp[i + 1][j - 1];
if (dp[i][j] && j - i + 1 > len) {
start = i;
len = j - i + 1;
}
}
}
return len === -1 ? s : s.slice(start, start + len);
};
复杂度
- 时间:n^2;
- 空间:n^2;
回文子串
题目
- 647;
思路
- 同最长回文子串;
- 初始值设置为字符串长度,
- 最大长度和起始位置替换为次数即可;
/**
* @param {string} s
* @return {number}
*/
var countSubstrings = function (s) {
const size = s.length;
const dp = Array.from(
{
length: size,
},
() => new Array(size).fill(false)
);
for (let i = 0; i < size; i++) {
dp[i][i] = true;
}
let res = 0;
for (let i = size - 1; i >= 0; i--) {
for (let j = i; j < size; j++) {
if (s[i] === s[j]) {
if (j - i <= 1) dp[i][j] = true;
else dp[i][j] = dp[i + 1][j - 1];
if (dp[i][j] === true) res++;
} else {
dp[i][j] = false;
}
}
}
return res;
};
复杂度
- 时间:n^2;
- 空间:n^2;
戳气球
题目
- 312;
思路
- 超出边界的气球为 1,因此数组两端添加两个数字为 1 的虚拟气球;
- 划分阶段:根据区间两端索引划分;
- 定义状态:
dp[i][j]表示戳破(i,j)区间所有气球获得的硬币数量; - 状态转移方程;
- 假设
(i,j)最后一个被戳破的气球索引为 k; dp[i][j]分割为dp[i][k] 和 dp[k][j];dp[i][j] = dp[i][k] + dp[k][j] + arr[i]*arr[j]*arr[k]
- 假设
- 初始条件:
dp[i][j] = 0; - 终止条件:
dp[0][size-1];
/**
* @param {number[]} nums
* @return {number}
*/
var maxCoins = function (nums) {
nums.push(1);
nums.unshift(1);
const size = nums.length;
const dp = Array.from(
{
length: size,
},
() => new Array(size).fill(0)
);
for (let l = 3; l <= size; l++) {
for (let i = 0; i < size; i++) {
j = i + l - 1;
if (j >= size) continue;
for (let k = i + 1; k < j; k++) {
dp[i][j] = Math.max(
dp[i][j],
dp[i][k] + dp[k][j] + nums[i] * nums[j] * nums[k]
);
}
}
}
return dp[0][size - 1];
};
复杂度
- 时间:n^3;
- 空间:n^2;
有效的括号字符串
题目
- 678;
思路
- 划分阶段:子串索引位置划分;
- 定义状态:dp[i][j] 为 s[i,j] 是否为有效字符串;
- 状态转移方程;
- 长度为 1:若 s[i] 为 *,可看做空字符串,dp[i][j] = true;
- 长度为 2:若两个字符串可分别看作
(),dp[i][j] = true; - 其余情况;
- 一个有效字符串:若两个字符串可分别看作
(),dp[i][j] = dp[i+1][j-1]; - 多个有效字符串:dp[i][j]=dp[i][k]&&dp[k+1][j];
- 一个有效字符串:若两个字符串可分别看作
- 起始条件:dp[i][j] = false;
- 终止条件:返回 dp[0][size-1];
/**
* @param {string} s
* @return {boolean}
*/
var checkValidString = function (s) {
const n = s.length;
const dp = Array.from(
{
length: n,
},
() => new Array(n).fill(false)
);
for (let i = n - 1; i >= 0; i--) {
for (let j = i; j < n; j++) {
if (i === j && s[i] === "*") dp[i][j] = true;
else if (
i + 1 === j &&
(s[i] === "(" || s[i] === "*") &&
(s[j] === ")" || s[j] === "*")
)
dp[i][j] = true;
else if (
(s[i] === "(" || s[i] === "*") &&
(s[j] === ")" || s[j] === "*")
) {
dp[i][j] = dp[i + 1][j - 1];
for (let k = i; k < j; k++) {
if (dp[i][j]) break;
dp[i][j] = dp[i][k] && dp[k + 1][j];
}
}
}
}
return dp[0][n - 1];
};
复杂度
- 时间:n^3;
- 空间:n^2;