数组
数组
基础
数组
- 相同类型元素;
- 线性数据结构;
优点
- 通过内存地址 O(1) 时间复杂度直接访问;
缺点
- 初始化长度不可变;
- 超过数组范围元素丢失;
- 内存浪费;
- 插入和删除效率低;
- 时间复杂度为 O(n);
数组基础题目
轮转数组
问题
- 189;
思路
- 数组元素向右移动 k 次后;
- 尾部 k mod n 个元素移动至头部,其余后移 k mod n 个位置;
- 翻转思路;
- 首先反转数组;
- 其次反转
[0, k % n - 1]; - 最后反转
[k % n, n - 1];
const reverse = (nums, start, end) => {
while (start < end) {
const temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start += 1;
end -= 1;
}
};
const rotate = function (nums, k) {
k %= nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
};
时间复杂度
- 时间:n;
- 空间:1;
对角线遍历
问题
- 498;
思路
- 一共 m + n - 1 跳对角线;
- 当 "行号 + 列号"为偶数,遍历顺序从左下到右上;
- 当为奇数,遍历顺序从右上的左下;
- 右上方移动时;
- 最后一列:向下移动;
- 第一行:向右移动:
- 其余:右上移动;
- 左下方移动时;
- 最后一行:向右移动;
- 第一列:向下移动;
- 其余:左下移动;
- 首先判断最后一行或最后一列,避免主对角线问题;
/**
* @param {number[][]} mat
* @return {number[]}
*/
var findDiagonalOrder = function (mat) {
const m = mat.length;
const n = mat[0].length;
const count = m * n;
let row = 0;
let col = 0;
const result = [];
for (let i = 0; i < count; i++) {
result.push(mat[row][col]);
if ((row + col) % 2 !== 1) {
if (col === n - 1) {
row += 1;
} else if (row === 0) {
col += 1;
} else {
col += 1;
row -= 1;
}
} else {
if (row === m - 1) {
col += 1;
} else if (col === 0) {
row += 1;
} else {
col -= 1;
row += 1;
}
}
}
return result;
};
复杂度
- 时间:m * n;
- 空间:m * n;
旋转图像
问题
- 048;
思路
mat[row][col]旋转后移动至mat[col][n-row-1];- 四次旋转;
- i,j/j,n-i-1,/n-i-1,n-j-1/n-j-1,i 形成一个循环;
- 使用 temp 缓存;
/**
* @param {number[][]} matrix
* @return {void} Do not return anything, modify matrix in-place instead.
*/
var rotate = function (matrix) {
const n = matrix.length;
for (let i = 0; i < Math.floor(n / 2); i++) {
for (let j = 0; j < Math.floor((n + 1) / 2); j++) {
const temp = matrix[i][j];
matrix[i][j] = matrix[n - j - 1][i];
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
matrix[j][n - i - 1] = temp;
}
}
};
复杂度
- 时间:n^2;
- 空间:1;
螺旋矩阵 1
问题
- 054;
思路
- 使用 ans 存储答案,定义四个边界;
- 按照顺时针顺序从边界访问元素;
- 访问完当前边界后,更新边界位置;
- 递归进行以上两步;
/**
* @param {number[][]} matrix
* @return {number[]}
*/
var spiralOrder = function (matrix) {
let left = 0;
let right = matrix[0].length - 1;
let top = 0;
let down = matrix.length - 1;
const result = [];
while (1) {
for (let i = left; i <= right; i++) {
result.push(matrix[top][i]);
}
top++;
if (top > down) {
break;
}
for (let i = top; i <= down; i++) {
result.push(matrix[i][right]);
}
right--;
if (left > right) {
break;
}
for (let i = right; i >= left; i--) {
result.push(matrix[down][i]);
}
down--;
if (top > down) {
break;
}
for (let i = down; i >= top; i--) {
result.push(matrix[i][left]);
}
left++;
if (left > right) {
break;
}
}
return result;
};
复杂度
- 时间:m * n;
- 空间:m * n;
螺旋矩阵 2
题目
- 059;
思路
- 同螺旋矩阵 1;
/**
* @param {number} n
* @return {number[][]}
*/
var generateMatrix = function (n) {
let left = 0;
let right = n - 1;
let top = 0;
let down = n - 1;
const result = new Array(n).fill(0).map(() => new Array(n).fill(0));
let num = 1;
while (1) {
for (let i = left; i <= right; i++) {
result[top][i] = num;
num++;
}
top++;
if (top > down) {
break;
}
for (let i = top; i <= down; i++) {
result[i][right] = num;
num++;
}
right--;
if (left > right) {
break;
}
for (let i = right; i >= left; i--) {
result[down][i] = num;
num++;
}
down--;
if (top > down) {
break;
}
for (let i = down; i >= top; i--) {
result[i][left] = num;
num++;
}
left++;
if (left > right) {
break;
}
}
return result;
};
复杂度
- 时间:n^2;
- 空间:n^2;
只出现一次的数字
问题
- 136;
思路
- 基于位运算中的异或操作;
- 遍历数组,递归进行异或操作,最终值即只出现一次的元素;
/**
* @param {number[]} nums
* @return {number}
*/
var singleNumber = function (nums) {
let ans = nums[0];
for (let i = 1; i < nums.length; i++) {
ans ^= nums[i];
}
return ans;
};
复杂度
- 时间:n;
- 空间:1;
列表
扩容机制
- 长度可变的数组;
- 当数组元素数量超过当前容量后;
- 容量扩充至当前 2 倍;
列表操作
访问
- 时间复杂度为 O(1);
插入
- 时间复杂度为 O(n);
删除
- 时间复杂度为 O(n);
添加
- 时间复杂度为 O(1);
- 扩容时为 O(n);
代码实现
export class List<T> {
capacity: number;
size: number;
array: T[];
constructor(capacity: number) {
this.capacity = capacity;
this.size = 0;
this.array = new Array(capacity);
}
get(index: number): T {
if (index >= this.size || index < 0) throw new Error("exceed");
return this.array[index];
}
insert(position: number, value: T): boolean {
if (position >= this.size || position < 0) throw new Error("exceed");
if (this.size === this.capacity) {
const array = new Array(2 * this.capacity);
this.capacity *= 2;
for (let index = 0; index < position; index++) {
const element = this.array[index];
array[index] = element;
}
array[position] = value;
for (let index = position; index < this.array.length; index++) {
const element = this.array[index];
array[index + 1] = element;
}
this.size++;
this.array = array;
return true;
}
for (let index = this.size - 1; index >= position; index--) {
const element = this.array[index];
this.array[index + 1] = element;
}
this.array[position] = value;
this.size++;
return true;
}
delete(position: number): T {
if (position >= this.size || position < 0) throw new Error("exceed");
const deleteElement = this.array[position];
for (let index = position + 1; index < this.array.length; index++) {
const element = this.array[index];
this.array[index - 1] = element;
}
this.size--;
return deleteElement;
}
append(value: T) {
if (this.size === this.capacity) {
const array = new Array(2 * this.capacity);
this.capacity *= 2;
for (let index = 0; index < this.array.length; index++) {
const element = this.array[index];
array[index] = element;
}
array[this.size] = value;
this.size++;
this.array = array;
return true;
}
this.array[this.size] = value;
this.size++;
return true;
}
}
数组排序
选择排序
工作原理
- 数组长度为 n;
- 选择 [0,n-1] 中最小的元素,与 0 处元素交换;
- 选择 [1,n-1] 中最小的元素,与 1 处元素交换;
- 依次类推,重复 n - 1 轮;
算法特性
- 时间复杂度:O(n^2);
- 空间复杂度:O(1);
- 非稳定排序;
代码
- 192;
/* 选择排序 */
function selectionSort(nums: number[]): void {
let n = nums.length;
// 外循环: 未排序区间为 [i, n-1]
for (let i = 0; i < n - 1; i++) {
// 内循环: 找到未排序区间内的最小元素
let k = i;
for (let j = i + 1; j < n; j++) {
if (nums[j] < nums[k]) {
k = j; // 记录最小元素的索引
}
}
// 将该最小元素与未排序区间的首个元素交换
[nums[i], nums[k]] = [nums[k], nums[i]];
}
}
冒泡排序
工作原理
- 从数组最左端开始向右遍历,若'左元素>右元素',交换两者;
- 数组长度为 n;
- 首先对 n 个元素进行冒泡,最大元素交换至最后位置;
- 其次对 n -1 个元素进行冒泡,第二大元素交换至倒数第二位置;
- 依次类推,重复 n - 1 轮;
算法特性
- 时间复杂度:O(n^2);
- 空间复杂度:O(1);
- 稳定排序;
代码
- 192;
/* 冒泡排序 */
function bubbleSort(nums: number[]): void {
// 外循环: 未排序区间为 [0, i]
for (let i = nums.length - 1; i > 0; i--) {
// 内循环: 将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
for (let j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
// 交换 nums[j] 与 nums[j + 1]
let tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
}
}
}
}
插入排序
工作原理
- 数组长度为 n;
- 数组第 1 个元素已完成排序;
- 选取数组第 2 个元素,与排序部分 (第 1 个元素) 比较,插入正确位置;
- 选取数组第 3 个元素,与排序部分 (前 2 个元素) 比较,插入正确位置;
- 依次类推,重复 n - 1 次;
算法特性
- 时间复杂度:O(n^2);
- 空间复杂度:O(1);
- 稳定排序;
插入排序优势
- 适用于小数据量;
- 冒泡排序涉及交换元素,开销高;
- 选择排序不稳定;
代码
- 192;
/* 插入排序 */
function insertionSort(nums: number[]): void {
// 外循环: 已排序元素数量为 1, 2, ..., n
for (let i = 1; i < nums.length; i++) {
const base = nums[i];
let j = i - 1;
// 内循环: 将 base 插入到已排序部分的正确位置
while (j >= 0 && nums[j] > base) {
nums[j + 1] = nums[j]; // 将 nums[j] 向右移动一位
j--;
}
nums[j + 1] = base; // 将 base 赋值到正确位置
}
}
希尔排序
工作原理
- 插入排序的改进;
- 按照一定间隔,划分为若干数组,对子数组进行插入排序;
- 不断缩小间隔,递归执行上一步,直至间隔为 1;
算法特性
- 时间:n*log2n - n^2;
- 空间:1;
- 非稳定排序;
代码
- 此处 gap 不断除以 2,时间复杂度为 n^2,但实现简单;
- 192;
const shellSort = (nums) => {
let gap = Math.floor(nums.length / 2);
while (gap > 0) {
for (let i = gap; i < nums.length; i++) {
const base = nums[i];
let j = i - gap;
while (j >= 0 && nums[j] > base) {
nums[j + gap] = nums[j];
j -= gap;
}
nums[j + gap] = base;
}
gap = Math.floor(gap / 2);
}
};
快速排序
哨兵划分
- 选取数组最左端作为 base,两个标识符 start,end 执行数组两端;
- 首先 end 向左寻找第一个小于 base 的元素;
- 其次 start 向右寻找第一个大于 base 的元素;
- 交换两个元素;
- 重复以上步骤,直至 start 和 end 相遇;
- base 设置为 start;
- 哨兵划分完成后,数组被划分成三部分,左子数组,基准数,右子数组,且左子数组 < 基准数 < 右子数组;
快速排序
- 对原数组进行哨兵排序;
- 对左子数组和右子数组递归执行哨兵排序,直至所有子数组长度为 1;
算法特性
- 时间复杂度:O(nlogn),最差为 O(n^2);
- 空间复杂度:O(n);
- 非稳定排序;
代码
- 192;
/* 元素交换 */
swap(nums: number[], i: number, j: number): void {
let tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
/* 哨兵划分 */
partition(nums: number[], left: number, right: number): number {
// 以 nums[left] 为基准数
let i = left,
j = right;
while (i < j) {
while (i < j && nums[j] >= nums[left]) {
j -= 1; // 从右向左找首个小于基准数的元素
}
while (i < j && nums[i] <= nums[left]) {
i += 1; // 从左向右找首个大于基准数的元素
}
// 元素交换
this.swap(nums, i, j); // 交换这两个元素
}
this.swap(nums, i, left); // 将基准数交换至两子数组的分界线
return i; // 返回基准数的索引
}
/* 快速排序 */
quickSort(nums: number[], left: number, right: number): void {
// 子数组长度为 1 时终止递归
if (left >= right) {
return;
}
// 哨兵划分
const pivot = this.partition(nums, left, right);
// 递归左子数组, 右子数组
this.quickSort(nums, left, pivot - 1);
this.quickSort(nums, pivot + 1, right);
}
归并排序
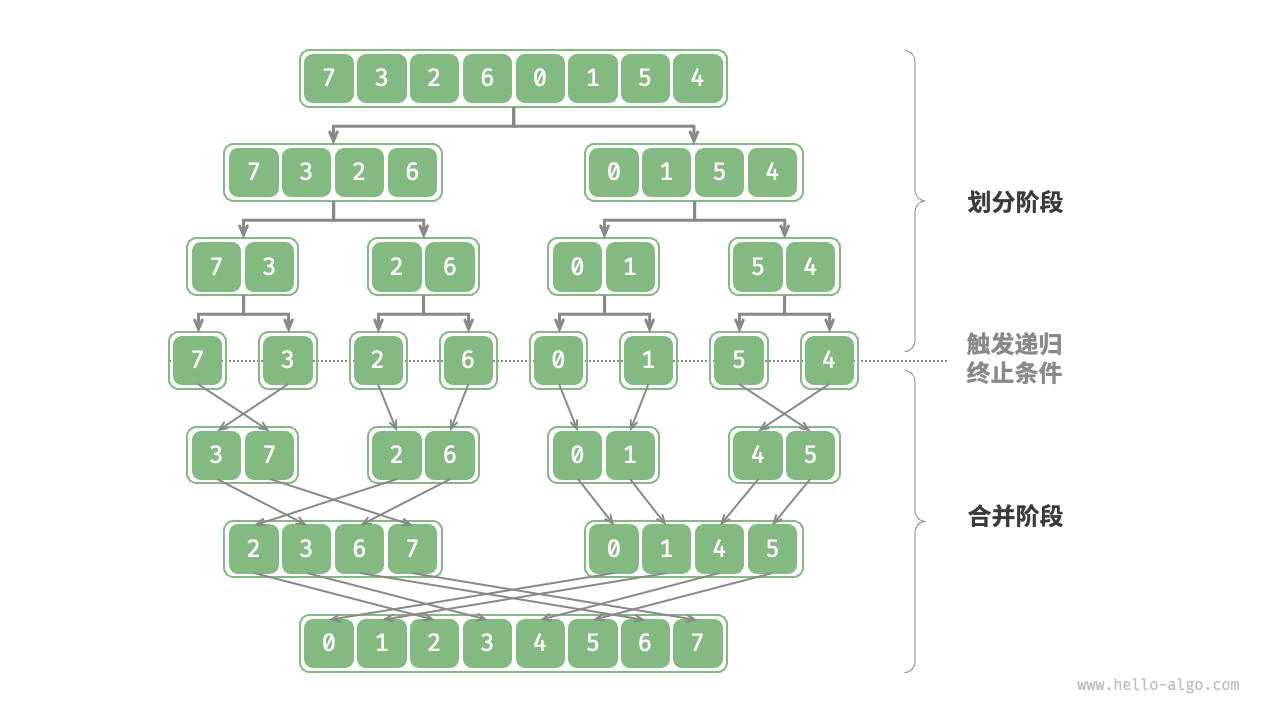
工作原理
- 划分阶段;
- 通过递归从中点划分数组;
- 首先递归左子数组,其次右子数组,最后合并;
- 合并阶段;
- 当子数组长度为 1 时终止递归;
- 持续的将左右较短的有序数组排序并合并为较长的有序数组;
算法特性
- 时间复杂度:O(nlongn);
- 空间复杂度:O(n);
- 稳定排序;
代码
- 192;
/* 合并左子数组和右子数组 */
function merge(nums, left, mid, right) {
// 左子数组区间为 [left, mid], 右子数组区间为 [mid+1, right]
const tmp = new Array(right - left + 1);
// 初始化左子数组和右子数组的起始索引
let i = left;
let j = mid + 1;
let k = 0;
// 当左右子数组都还有元素时, 进行比较并将较小的元素复制到临时数组中
while (i <= mid && j <= right) {
if (nums[i] <= nums[j]) {
tmp[k++] = nums[i++];
} else {
tmp[k++] = nums[j++];
}
}
// 将左子数组和右子数组的剩余元素复制到临时数组中
while (i <= mid) {
tmp[k++] = nums[i++];
}
while (j <= right) {
tmp[k++] = nums[j++];
}
// 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间
for (k = 0; k < tmp.length; k++) {
nums[left + k] = tmp[k];
}
}
/* 归并排序 */
function mergeSort(nums, left, right) {
// 终止条件
if (left >= right) return; // 当子数组长度为 1 时终止递归
// 划分阶段
let mid = Math.floor((left + right) / 2); // 计算中点
mergeSort(nums, left, mid); // 递归左子数组
mergeSort(nums, mid + 1, right); // 递归右子数组
// 合并阶段
merge(nums, left, mid, right);
}
堆排序
工作原理
- 基于输入数组建立大顶堆;
- 堆顶元素和堆底元素交换,交换完成后,堆长度 -1,排序元素长度 +1;
- 从顶到底执行自顶向下的交换操作,重新建立堆;
- 循环执行以上 2 步,n-1 轮后完成数组排序;
算法特性
- 时间复杂度:O(nlongn);
- 空间复杂度:O(1);
- 非稳定排序;
代码
- 192;
/* 堆的长度为 n , 从节点 i 开始, 从顶至底堆化 */
function siftDown(nums, n, i) {
while (true) {
// 判断节点 i, l, r 中值最大的节点, 记为 ma
let l = 2 * i + 1;
let r = 2 * i + 2;
let ma = i;
if (l < n && nums[l] > nums[ma]) {
ma = l;
}
if (r < n && nums[r] > nums[ma]) {
ma = r;
}
// 若节点 i 最大或索引 l, r 越界, 则无须继续堆化, 跳出
if (ma === i) {
break;
}
// 交换两节点
[nums[i], nums[ma]] = [nums[ma], nums[i]];
// 循环向下堆化
i = ma;
}
}
/* 堆排序 */
function heapSort(nums) {
// 建堆操作: 堆化除叶节点以外的其他所有节点
for (let i = Math.floor(nums.length / 2) - 1; i >= 0; i--) {
siftDown(nums, nums.length, i);
}
// 从堆中提取最大元素, 循环 n-1 轮
for (let i = nums.length - 1; i > 0; i--) {
// 交换根节点与最右叶节点 (交换首元素与尾元素)
[nums[0], nums[i]] = [nums[i], nums[0]];
// 以根节点为起点, 从顶至底进行堆化
siftDown(nums, i, 0);
}
}
桶排序
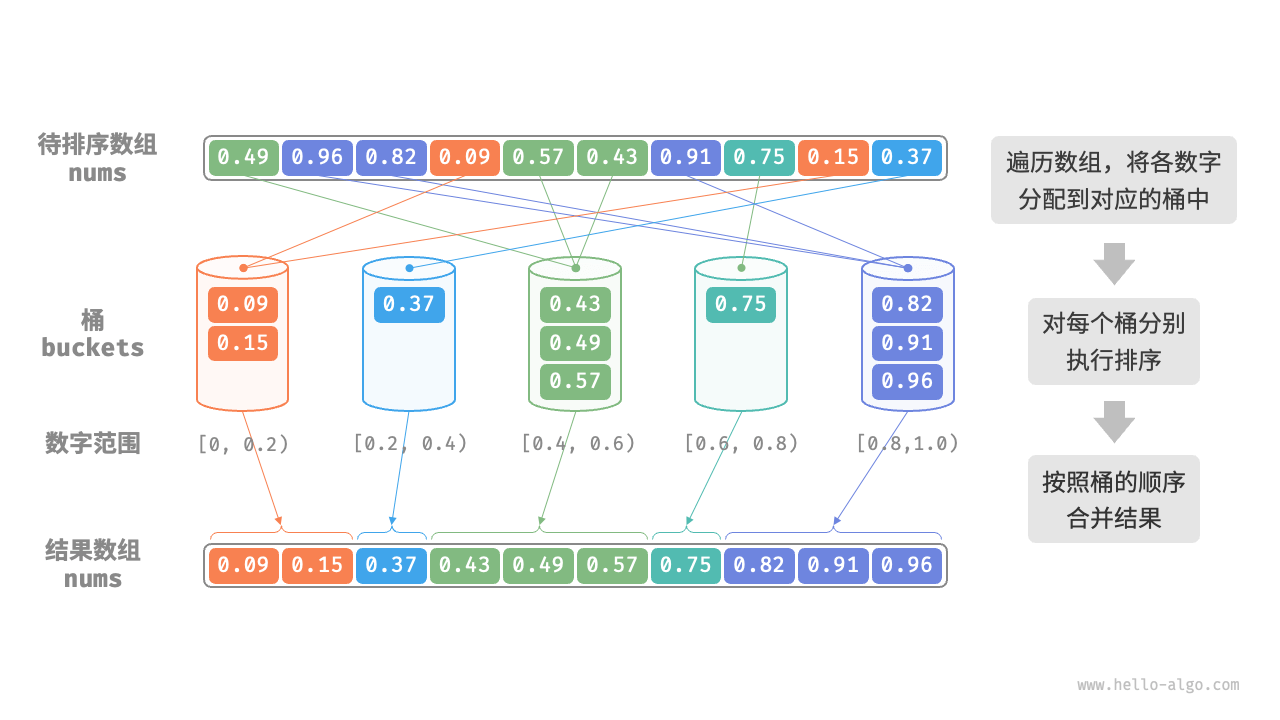
工作原理
- 长度为 n 的整数数组;
- 初始化 k 个桶,将 n 个元素分配到 k 个桶中;
- 对每个桶分别进行排序;
- 根据桶的大小合并结果;
算法特性
- 时间复杂度:O(n + k);
- 排序需要 n;
- 合并需要 k;
- 空间复杂度:O(n + k);
- k 个桶;
- n 个元素;
应用场景
- 针对有限范围内的数字,或通过 hash 转换为数字;
代码
- 192;
/* 桶排序 */
function bucketSort(nums, size) {
// 初始化 k 个桶
const k = Math.floor(nums.length / size);
const buckets = [];
for (let i = 0; i < k; i++) {
buckets.push([]);
}
// 1. 将数组元素分配到各个桶中
const min = Math.min(...nums);
const range = Math.max(...nums) - min;
// 判断数组长度或者数组是否都是一个值
if (range === 0) return;
for (const num of nums) {
const i = Math.floor(((num - min) / range) * (k - 1));
buckets[i].push(num);
}
// 2. 对各个桶执行排序
for (const bucket of buckets) {
// 使用内置排序函数, 也可以替换成其他排序算法
bucket.sort((a, b) => a - b);
}
// 3. 遍历桶合并结果
let i = 0;
for (const bucket of buckets) {
for (const num of bucket) {
nums[i++] = num;
}
}
return nums;
}
计数排序
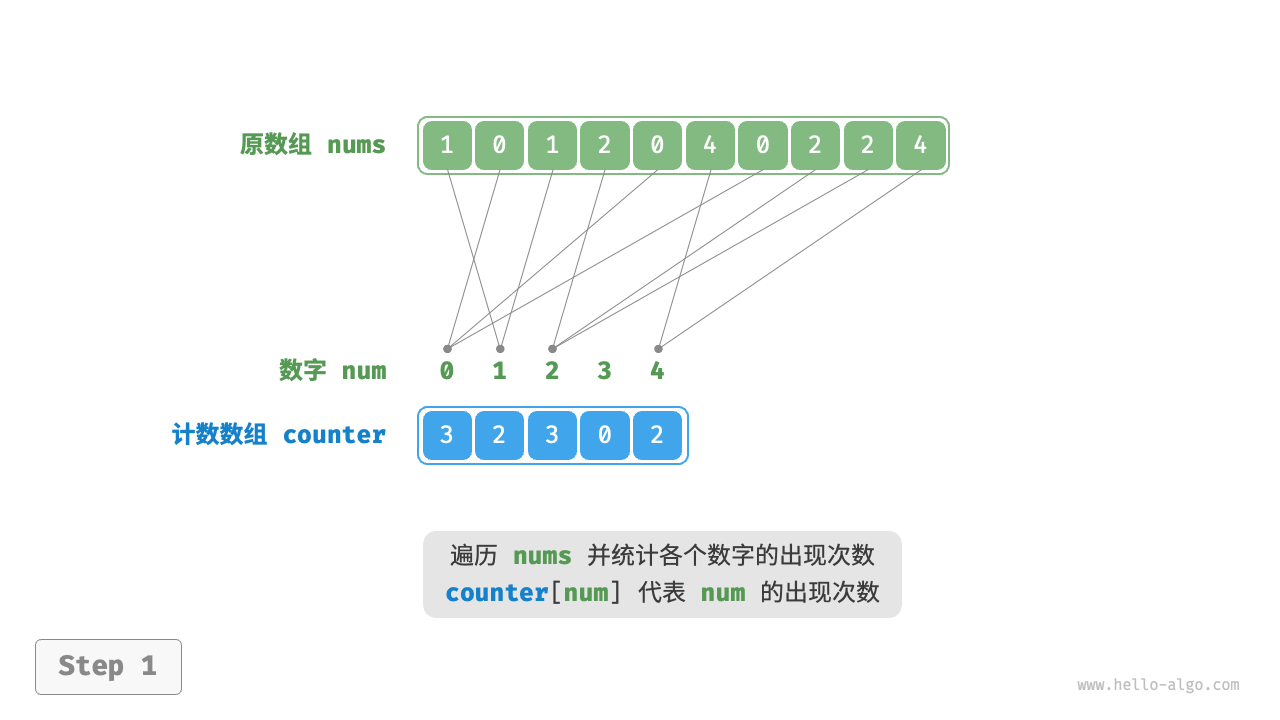
工作原理
- 给定长度 n 为整数数组 nums;
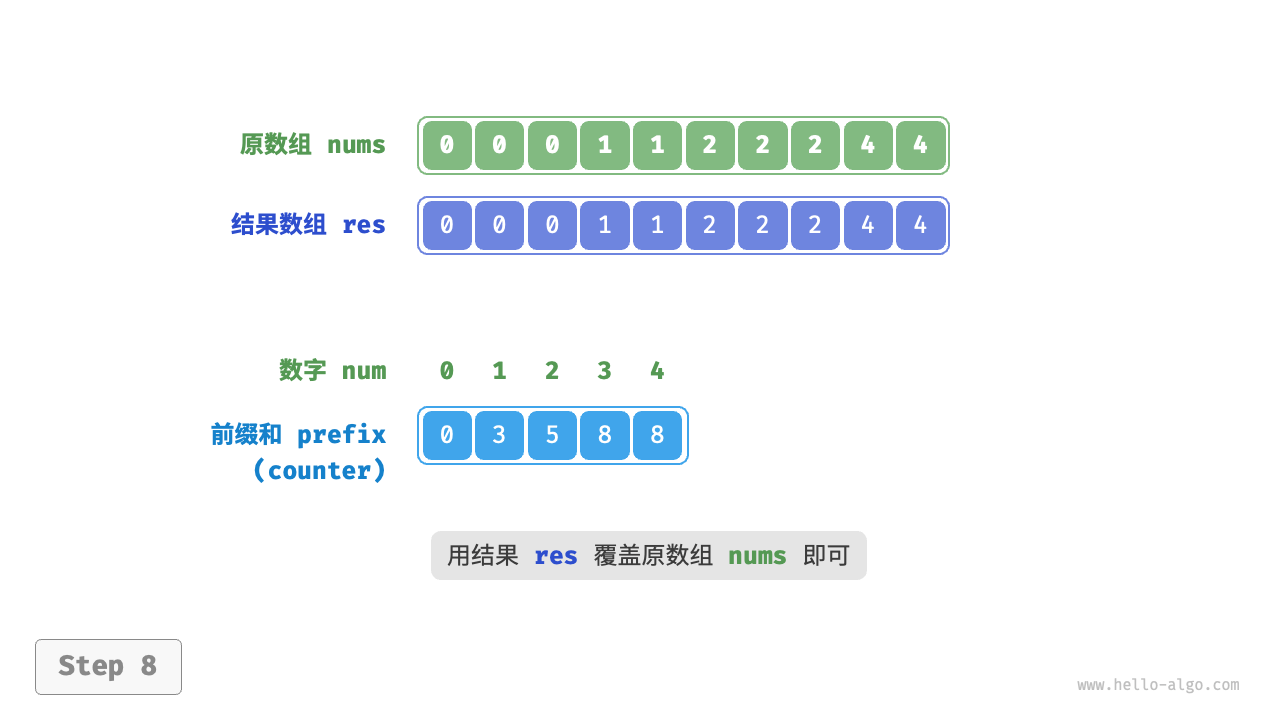
- 遍历数组,找出最大数字 m,创建一个 m + 1 的数组 counter;
- 统计 nums 中个数字出现的次数,counter[num] 对应 num 的出现次数;
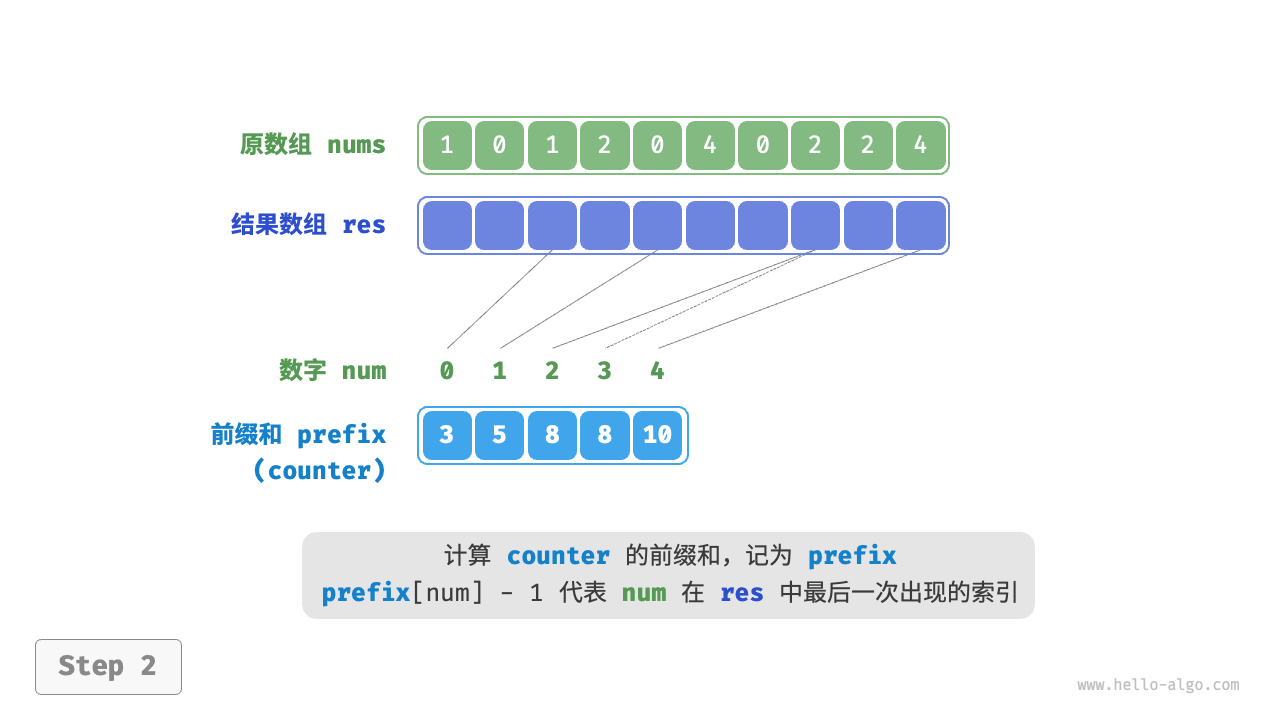
- 基于 counter 生成前缀和 prefix;
- prefix[i] = ;
- 倒序遍历 nums;
res[prefix[num]-1]=num;- prefix[num] -= 1;
算法特性
- 时间复杂度:O(n + m);
- 空间复杂度:O(n + m);
- 稳定排序;
计数排序和堆排序
- 可将 counter 的每个索引看作一个桶;
- 计数排序是桶排序在整数数组下的特例;
应用场景
- 正整数数组;
- 数据量大但数据范围小;
代码
- 192;
/**
* @param {number[]} nums
* @return {number[]}
*/
var sortArray = function (nums) {
const countingSort = (nums) => {
const max = Math.max(...nums);
const min = Math.min(...nums);
const counters = new Array(max - min + 1).fill(0);
for (const num of nums) {
counters[num - min]++;
}
for (let i = 0; i < counters.length - 1; i++) {
counters[i + 1] += counters[i];
}
const res = new Array(nums.length);
for (let i = 0; i < nums.length; i++) {
const value = nums[i];
res[counters[value - min] - 1] = value;
counters[value - min]--;
}
for (let i = 0; i < nums.length; i++) {
nums[i] = res[i];
}
};
countingSort(nums);
return nums;
};
基数排序
工作原理
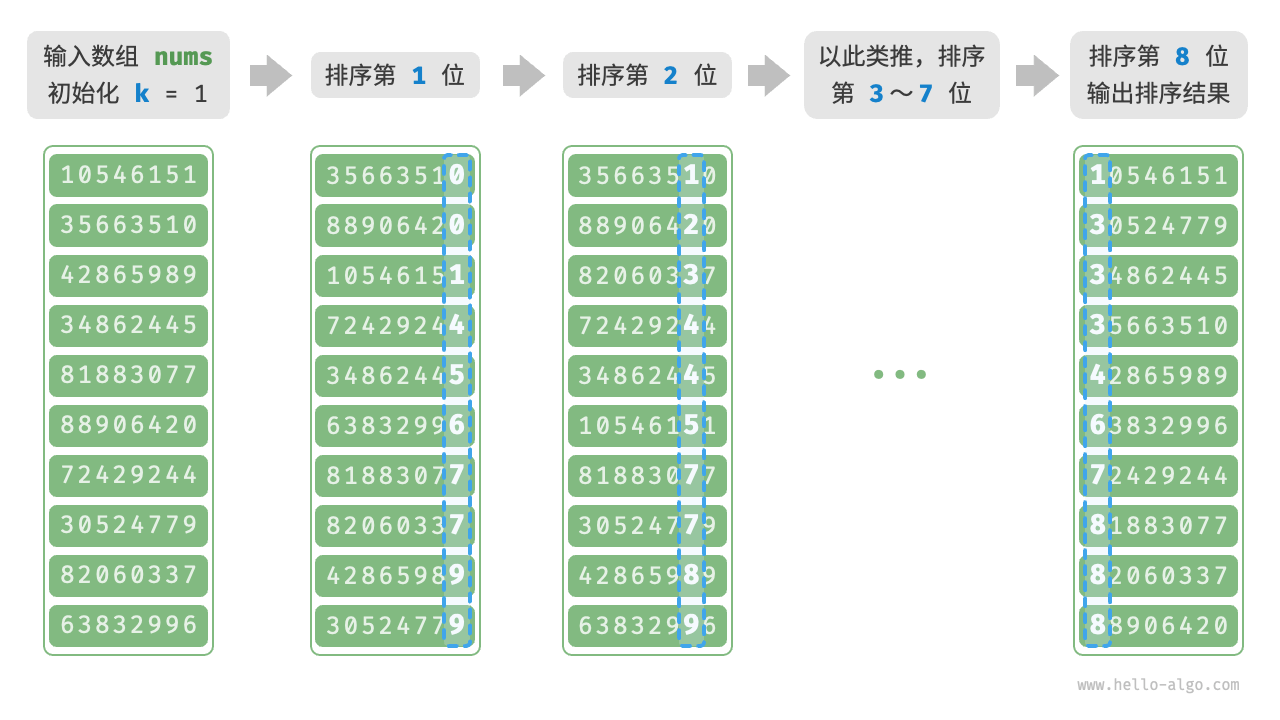
- 核心原理同计数排序,在计数排序的基础上,理由数字各位的递进关系,依次对每一位进行排序;
- 初始化 k = 1;
- 对数字第 k 位进行计数排序;
- k + 1,重复上一步骤,直至所有为排序完成;
算法特性
- 时间复杂度:O(nk);
- 空间复杂度:O(n + d);
- 稳定排序;
应用场景
- 数据范围大;
代码
- 192;
/* 获取元素 num 的第 k 位, 其中 exp = 10^(k-1) */
function digit(num, exp) {
// 传入 exp 而非 k 可以避免在此重复执行昂贵的次方计算
return Math.floor(num / exp) % 10;
}
/* 计数排序 (根据 nums 第 k 位排序) */
function countingSortDigit(nums, exp) {
// 十进制的位范围为 0~9 , 因此需要长度为 10 的桶数组
const counter = new Array(10).fill(0);
const n = nums.length;
// 统计 0~9 各数字的出现次数
for (let i = 0; i < n; i++) {
const d = digit(nums[i], exp); // 获取 nums[i] 第 k 位, 记为 d
counter[d]++; // 统计数字 d 的出现次数
}
// 求前缀和, 将 "出现个数" 转换为 "数组索引"
for (let i = 1; i < 10; i++) {
counter[i] += counter[i - 1];
}
// 倒序遍历, 根据桶内统计结果, 将各元素填入 res
const res = new Array(n).fill(0);
for (let i = n - 1; i >= 0; i--) {
const d = digit(nums[i], exp);
const j = counter[d] - 1; // 获取 d 在数组中的索引 j
res[j] = nums[i]; // 将当前元素填入索引 j
counter[d]--; // 将 d 的数量减 1
}
// 使用结果覆盖原数组 nums
for (let i = 0; i < n; i++) {
nums[i] = res[i];
}
}
/* 基数排序 */
function radixSort(nums) {
// 获取数组的最大元素, 用于判断最大位数
let m = Number.MIN_VALUE;
for (const num of nums) {
if (num > m) {
m = num;
}
}
// 按照从低位到高位的顺序遍历
for (let exp = 1; exp <= m; exp *= 10) {
// 对数组元素的第 k 位执行计数排序
// k = 1 -> exp = 1
// k = 2 -> exp = 10
// 即 exp = 10^(k-1)
countingSortDigit(nums, exp);
}
}
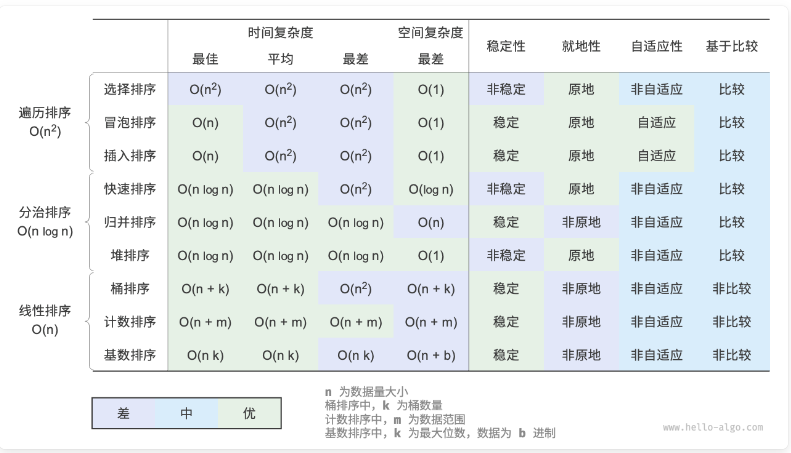
排序算法优劣
- 冒泡,选择,插入排序稳定;
- 时间 n^2,空间 1;
- 插入排序适合小数据量;
- 快速,归并,堆排序;
- 时间 nlogn;
- 快速:存在基准值劣化风险;
- 堆排序:空间复杂度低 1;
- 桶,计数排序;
- 时间 m+n,空间 m+n;
- 桶排序:适合大数据量;
- 计数排序:适合大数据量且取值范围有限;
- 基数排序:时间 nk,空间 n+b;
数组排序题目
数组中的第 K 个最大元素
题目
- 215;
思路
- 堆排序;
- 使用堆排序,堆排序每次排序后,便会得到当前最大的数;
- 当递归排序 k 次后,直接输出即可,无需排序整个数组;
- 其实我写的堆排序,百分百比自带排序慢;
- 快速排序;
- 每一次快速排序后,对于基准值的确定已经完成;
- 判断 mid 是否等于 n-k;
- 等于返回 mid;
- 小于递归 mid + 1,right;
- 大于递归 left,mid;
- 划分思路即二分查找;
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var findKthLargest = function (nums, k) {
const siftDown = (nums, n, i) => {
while (1) {
let left = 2 * i + 1;
let right = left + 1;
let temp = i;
if (left < n && nums[left] > nums[temp]) {
temp = left;
}
if (right < n && nums[right] > nums[temp]) {
temp = right;
}
if (temp === i) break;
[nums[temp], nums[i]] = [nums[i], nums[temp]];
i = temp;
}
};
const findK = (nums, k) => {
for (let i = nums.length - 1; i >= 0; i--) {
siftDown(nums, nums.length, i);
}
for (let i = nums.length - 1; i > nums.length - k; i--) {
[nums[0], nums[i]] = [nums[i], nums[0]];
siftDown(nums, i, 0);
}
};
findK(nums, k);
return nums[0];
};
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var findKthLargest = function (nums, k) {
const partition = (nums, left, right) => {
let i = left;
let j = right;
let index = Math.floor(Math.random() * (right - left + 1) + left);
[nums[left], nums[index]] = [nums[index], nums[left]];
while (i < j) {
while (i < j && nums[j] >= nums[left]) j--;
while (i < j && nums[i] <= nums[left]) i++;
[nums[i], nums[j]] = [nums[j], nums[i]];
}
[nums[i], nums[left]] = [nums[left], nums[i]];
return i;
};
const quickSort = (nums, left, right) => {
if (left >= right) return nums[left];
const mid = partition(nums, left, right);
if (mid === nums.length - k) return nums[mid];
else if (mid > nums.length - k) {
return quickSort(nums, left, mid);
} else {
return quickSort(nums, mid + 1, right);
}
};
return quickSort(nums, 0, nums.length - 1);
};
复杂度
- 时间:n * logn;
- 空间:1;
排序数组
问题概述
- 912;
思路
- 经典的排序算法即可;
合并区间
问题
- 56;
思路
- 首先根据 intervals 的区间左端点进行升序排序;
- 遍历所有区间;
- 如果区间左端点在前一区间右端点右侧,两区间不重合,直接添加;
- 反之两者重合,判断两个区间的右区间值大小,更新前一区间的右端点值;
/**
* @param {number[][]} intervals
* @return {number[][]}
*/
var merge = function (intervals) {
intervals = intervals.sort((a, b) => a[0] - b[0]);
let res = [intervals[0]];
for (let i = 1; i < intervals.length; i++) {
const current = intervals[i];
const before = res[res.length - 1];
if (current[0] > before[1]) {
res.push(current);
} else {
before[1] = Math.max(before[1], current[1]);
}
}
return res;
};
复杂度
- 时间:n * logn;
- 空间:n;
颜色分类
题目
- 75;
思路
- 最简单算法:任何一个排序算法即可;
- 进阶:快速排序 + 双指针;
- 将 1 作为基准数;
- 定义首尾指针 left,right;
- 遍历数组,当前索引为 index;
- 若为 0,交换 index 和 left,left++;
- 若为 1,不做任何操作;
- 若为 2,交换 index 和 right,right--;
- 直至 index 移动到 right 位置;
/**
* @param {number[]} nums
* @return {void} Do not return anything, modify nums in-place instead.
*/
var sortColors = function (nums) {
let left = 0;
let right = nums.length - 1;
for (let i = 0; i <= right; i++) {
if (nums[i] === 0) {
[nums[i], nums[left]] = [nums[left], nums[i]];
left++;
} else if (nums[i] === 1) {
continue;
} else {
[nums[i], nums[right]] = [nums[right], nums[i]];
right--;
i--;
}
}
};
复杂度
- 时间:n;
- 空间:1;
最大数
问题
- 179;
思路
- 假设 x,y 为数组相邻两个元素;
- 拼接字符串
xy和yx,利用字符串比较规则 (逐字符比较编码顺序),判断大小; - 选择较大数字对应的 xy 顺序;
- 拼接字符串
- 通过大小为 2 的滑动窗口,遍历数组,根据以上比较规则,更改数组顺序;
/**
* @param {number[]} nums
* @return {string}
*/
var largestNumber = function (nums) {
nums.sort((a, b) => {
if (`${a}${b}` < `${b}${a}`) {
return 1;
} else {
return -1;
}
});
if (nums[0] === 0) return "0";
return nums.join("");
};
复杂度
- 时间:根据字符串的比较算法不同而不同;
- 假设比较算法时间复杂度为 a;
- 时间复杂度为 n * a;
- 空间:n;
最大间距
题目
- 164;
思路
- 使用复杂度为 n 的排序算法即可;
- 堆/基数/计数/桶;
- 因为本题为正整数,使用桶排序和基数排序皆可;
/**
* @param {number[]} nums
* @return {number}
*/
var maximumGap = function (nums) {
const bucketSort = (nums, size) => {
const k = Math.floor(nums.length / 3);
const bucketList = [];
for (let i = 0; i < k + 1; i++) {
bucketList.push([]);
}
const min = Math.min(...nums);
const range = Math.max(...nums) - min;
if (range === 0) return nums;
for (let i = 0; i < nums.length; i++) {
const num = nums[i];
const index = Math.floor(((num - min) / range) * k);
bucketList[index].push(num);
}
for (let i = 0; i < bucketList.length; i++) {
const bucket = bucketList[i];
bucket.sort((a, b) => a - b);
}
const res = [];
for (let i = 0; i < bucketList.length; i++) {
const bucket = bucketList[i];
res.push(...bucket);
}
return res;
};
if (nums.length < 2) return 0;
const arr = bucketSort(nums, 3);
let res = -Infinity;
for (let i = 1; i < arr.length; i++) {
res = Math.max(res, arr[i] - arr[i - 1]);
}
return res;
};
复杂度
- 时间:n;
- 空间:n;
打乱数组
题目
- 384 ;
思路
- 该问题可转换为,n 个位置,选择填入某个数的概率相同,即洗牌算法;
- 洗牌算法;
- 对于第 0 个位置,选择 0 - n - 1 的随机数,交换位置;
- 对于第 1 个位置,选择 1 - n - 1 的随机数,交换位置;
- 以此类推;
/**
* @param {number[]} nums
*/
var Solution = function (nums) {
this.state = nums;
this.origin = [...nums];
};
/**
* @return {number[]}
*/
Solution.prototype.reset = function () {
this.state = [...this.origin];
return this.state;
};
/**
* @return {number[]}
*/
Solution.prototype.shuffle = function () {
const arr = this.state;
for (let i = arr.length - 1; i >= 0; i--) {
const index = Math.floor(Math.random() * (i + 1));
[arr[i], arr[index]] = [arr[index], arr[i]];
}
return arr;
};
/**
* Your Solution object will be instantiated and called as such:
* var obj = new Solution(nums)
* var param_1 = obj.reset()
* var param_2 = obj.shuffle()
*/
数组中的逆序对
题目
思路
- 基于归并排序;
- 定义 count 维护逆序对数量;
- 当
nums[i] > nums[j],说明nums[i,mid]都大于,因此 count+=mid-i+1;
/**
* @param {number[]} record
* @return {number}
*/
var reversePairs = function (record) {
function merge(nums, left, mid, right) {
const tmp = new Array(right - left + 1);
let i = left;
let j = mid + 1;
let k = 0;
while (i <= mid && j <= right) {
if (nums[i] <= nums[j]) {
tmp[k++] = nums[i++];
} else {
tmp[k++] = nums[j++];
res += mid - i + 1;
}
}
while (i <= mid) {
tmp[k++] = nums[i++];
}
while (j <= right) {
tmp[k++] = nums[j++];
}
for (k = 0; k < tmp.length; k++) {
nums[left + k] = tmp[k];
}
}
function mergeSort(nums, left, right) {
if (left >= right) return;
let mid = Math.floor((left + right) / 2);
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
merge(nums, left, mid, right);
}
let res = 0;
mergeSort(record, 0, record.length - 1);
return res;
};
复杂度
- 时间:nlogn;
- 空间:n;
二分查找
基础
中间值
- mid = Math.floor(left + (right-left)/2);
- 避免极大值超出 int 的影响;
旋转排序数组总体思路
- 旋转数组具有一段有序或两端有序;
- 一段有序也可看作两端有序;
- 故统一为两端有序;
- 计算中间节点 mid,向下取整;
- 比较 nums[mid] 和 nums[right];
- 因为 mid 向下取整,所以 mid !== right;
- nums[mid] > nums[right],左半部分,right = mid - 1;
- 反之右半部分,left = mid + 1;
等于号问题
- 一律使用 left < right;
区间问题
- 由于使用 left < right,此时区间为 [left,right);
- right 为开区间,所以初始 right 从 nums.length 开始;
- 如果第一次比较需要使用 right,right 从 nums.length-1 开始;
mid 问题
- 由于 left 为闭区间,right 为开区间,基于 mid 缩小范围时;
- left 往往是 mid + 1,right 往往是 mid;
left 取值问题
- 终止条件;
- 由于使用 left < right,终止条件为 left === right;
- 此次返回结果为 [left,right],区间中仍存在结果;
- 如果结果值可能不存在,需要在循环外对 nums[left] 进行判断;
- 边界条件;
- 由于 left 为闭区间,且 left 往往为 mid + 1;
- 当 mid 为数组最后一个元素时,且对应情况取值 left = mid + 1;
- left 为超出数组索引范围,需要对 left-1 进行检查;
- 如果结果可能不存在,循环外需要对 left 进行索引检查;
- 由于 left 为闭区间,且 left 往往为 mid + 1;
二分查找题目
二分查找
题目
- 给定升序数组 nums,和目标值 target;
- nums 元素不重复;
- 返回 target 在 nums 的索引,不存在返回 -1;
- 704;
思想
- 初始化指针 start = 0 和 end = n;
- 取中点 m = Math.floor((start + end) / 2);
- 判断 arr[m] 与 target 的关系;
- 若
arr[m] < target,start = m + 1; - 若 arr[m] > target,end = m;
- 若 arr[m] = target,返回 m;
- 若
- 循环结束条件为 start >= end,寻找判断 nums[start] === target;
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var search = function (nums, target) {
let left = 0;
let right = nums.length;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
if (target === nums[mid]) {
return mid;
} else if (target < nums[mid]) {
right = mid;
} else {
left = mid + 1;
}
}
if (nums[left] === target) return left;
return -1;
};
复杂度
- 时间:logn;
- 空间:1;
二分查找插入点
适用场景
- 给定升序 (降序)数组;
- 将 target 插入数组中,并保持升序 (降序);
数组无重复元素
- 使用二分查找搜索 target;
- 若数组存在 target,插入其左边,即 target 所处位置,返回 m;
- 若数组不存在 target,插入首个大于 target 的元素的位置,即 start,返回 start;
export const binarySearchInsertion = (
numArray: number[],
target: number
): number => {
let start = 0;
let end = numArray.length;
while (start <= end) {
const currentIndex = Math.floor((start + end) / 2);
const value = numArray[currentIndex];
if (value > target) {
end = currentIndex - 1;
} else if (value === target) {
return currentIndex;
} else {
start = currentIndex + 1;
}
}
return start;
};
数组存在重复元素
- 基于二分查找的实现;
- 若数组不存在 target,插入首个大于 target 的元素的位置,即 start,返回 start;
- 若数组存在 target,插入其左边,即最左边 target 的元素的位置;
- 当 value > target 或 value = target 时;
- 首个小于 target 的元素必然在 [start,m - 1] 区间中;
- 当 start > end 时,start 指向最左边的 target;
- 故返回 start;
export const binarySearchInsertion = (
numArray: number[],
target: number
): number => {
let start = 0;
let end = numArray.length;
while (start <= end) {
const mid = Math.floor((start + end) / 2);
if (target <= nums[mid]) {
end = mid - 1;
} else {
start = mid + 1;
}
}
return start;
};
在排序数组中查找元素的第一个和最后一个位置
问题
- 034;
思想
- 若数组不存在 target,start 指向首个大于 target 的位置,返回 -1;
- 左边界;
- 若数组存在 target,返回最左边 target 的元素的位置;
- 当 value > target 或 value = target 时,最左 target 的元素必然在 [start,m - 1] 区间中,故 right = mid;
- 当 value < target 时,最左 target 的元素必然在 [m+ 1,end] 区间中,left = mid + 1;
- 当 start > end 时,start 指向最左边的 target;
- 若数组存在 target,返回最左边 target 的元素的位置;
- 右边界;
- 若数组存在 target,返回最右边 target 元素位置;
- 当 value < target 或 value = target 时,最右 target 的元素必然在 [m + 1,end] 区间中,left = mid + 1;
- 当 value > target 时,最右 target 的元素必然在 [start,m - 1] 区间中,right = mid;
- 当 start > end 时,start 指向大于 target 的第一个元素;
- 若数组存在 target,返回最右边 target 元素位置;
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
var searchRange = function (nums, target) {
const res = [-1, -1];
let left = 0;
let right = nums.length;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
if (nums[mid] === target) right = mid;
else if (nums[mid] > target) right = mid;
else left = mid + 1;
}
if (nums[left] === target) res[0] = left;
left = 0;
right = nums.length;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
if (nums[mid] === target) left = mid + 1;
else if (nums[mid] > target) right = mid;
else left = mid + 1;
}
if (nums[left - 1] === target) res[1] = left - 1;
return res;
};
复杂度
- 时间:log2n;
- 空间:1;
寻找旋转排序数组中的最小值 1
题目
- 153;
思路
- 数组旋转后,两种排序情况;
- 原先的排序:最小值为第一个元素;
- 两端升序的序列;
- 第一段整体大于第二段;
- 最小值为第二段升序的第一个元素;
- 创建指针 start,end;
- 计算中间指针 mid;
- 若
nums[mid] > nums[right],最小值不可能在 mid 左侧,left = mid + 1; - 若
nums[mid] <= nums[right],最小值一定在 mid 或 mid 左侧,right = mid;
- 若
- 直至 left = right,此时对应值即最小值;
/**
* @param {number[]} nums
* @return {number}
*/
var findMin = function (nums) {
let start = 0;
let end = nums.length - 1;
while (start < end) {
const mid = Math.floor((start + end) / 2);
if (nums[mid] === nums[end]) {
end = mid;
} else if (nums[mid] < nums[end]) {
end = mid;
} else {
start = mid + 1;
}
}
return nums[left];
};
复杂度
- 时间:logn;
- 空间:1;
寻找旋转排序数组中的最小值 2
题目
- 154;
思路
- 类似寻找旋转排序数组中的最小值 1;
- 创建指针 start,end;
- 计算中间指针 mid;
- 若 nums[mid] > nums[right],最小值不可能在 mid 左侧,left = mid + 1;
- 若 nums[mid] < nums[right],最小值一定在 mid 或 mid 左侧,right = mid;
- 若 nums[mid] === nums[right];
- 由于数字可能存在重复元素,nums[right] 可能横跨数组末端和开头;
- 无法判断最小值在 right 左端还是右端;
- 直接 right -= 1;
- 如果 nums[mid] 为最小值,因为 mid < right,仍在二分区间内;
- 反之 nums[mid] 不是最小值,即最小值必然在 mid 左侧,right-- 排除错误答案;
- 巧妙算法;
- 直接排除重复元素横跨数组的情况,将 left 放置于第一个不等于 nums[-1] 的位置;
- 其余直接同寻找旋转排序数组中的最小值 1;
/**
* @param {number[]} nums
* @return {number}
*/
var findMin = function (nums) {
let start = 0;
let end = nums.length - 1;
while (start < end) {
const mid = Math.floor((start + end) / 2);
if (nums[mid] === nums[end]) {
end -= 1;
} else if (nums[mid] < nums[end]) {
end = mid;
} else {
start = mid + 1;
}
}
return nums[left];
};
/**
* @param {number[]} nums
* @return {number}
*/
var findMin = function (nums) {
let start = 0;
let end = nums.length - 1;
while (start < end && nums[start] === nums[end]) start++;
while (start < end) {
const mid = Math.floor((start + end) / 2);
if (nums[mid] === nums[end]) {
end = mid;
} else if (nums[mid] < nums[end]) {
end = mid;
} else {
start = mid + 1;
}
}
return nums[left];
};
复杂度
- 时间:logn;
- 空间:1;
搜索旋转数组 1
题目
- 33;
思路
- 数组旋转后,两种排序情况;
- 原先的排序:最小值为第一个元素;
- 两端升序的序列;
- 第一段整体大于第二段;
- 最小值为第二段升序的第一个元素;
- 创建指针 start,end;
- 计算中间指针 mid;
- 若 nums[mid] = target,返回下标;
- 若 nums[mid] > num[right],mid 在左半部分;
- 如果 target < nums[mid] && target >= nums[left],target 位于 [left,mid-1];
- 反之 target 位于 [mid+1,right]
- 若 nums[mid] < nums[left],mid 在右半部分;
- 参考以上思路;
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var search = function (nums, target) {
let left = 0;
let right = nums.length - 1;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
if (nums[mid] === target) return mid;
else if (nums[mid] > nums[right]) {
if (target >= nums[left] && target <= nums[mid]) right = mid;
else left = mid + 1;
} else {
if (target >= nums[mid] && target <= nums[right]) left = mid + 1;
else right = mid;
}
}
if (nums[left] === target) return left;
return -1;
};
复杂度
- 时间:logn;
- 空间:1;
寻找峰值
问题
- 162;
思路
- 因为相邻元素不相等,因此沿着上升方向,一定可以找到峰值;
- 使用两端指针 left,right;
- 取中间节点 mid,比较 nums[mid] 和 mid[mid + 1];
- 若 nums[mid] < nums[mid+1],右侧必然存在峰值,left = mid + 1;
- 反之左侧存在峰值,right = mid;
/**
* @param {number[]} nums
* @return {number}
*/
var findPeakElement = function (nums) {
let left = 0;
let right = nums.length - 1;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
if (nums[mid] > nums[mid + 1]) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
};
复杂度
- 时间:logn;
- 空间:1;
搜索二维矩阵 1
题目
- 74;
思路
- 使用两次二分查找;
- 第一次定位行;
- target > matrix[mid][0] 时,需要对 matrix[mid][-1] 进行二次比较;
- 如果 target > matrix[mid][-1],left=mid+1;
- 反之即本行,left = mid,并跳出循环;
- 需要对 row 范围进行检查;
- 第二次定位列;
- 第一次定位行;
- 双指针;
- 同搜索二维矩阵 2;
- 故不列具体代码;
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
var searchMatrix = function (matrix, target) {
const m = matrix.length;
const n = matrix[0].length;
let left = 0;
let right = m;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
if (target === matrix[mid][0]) {
return true;
} else if (target < matrix[mid][0]) {
right = mid;
} else {
if (target <= matrix[mid][n - 1]) {
left = mid;
break;
} else {
left = mid + 1;
}
}
}
if (left >= m) return false;
const row = left;
left = 0;
right = n;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
if (target === matrix[row][mid]) {
return true;
} else if (target < matrix[row][mid]) {
right = mid;
} else {
left = mid + 1;
}
}
return false;
};
复杂度
- 时间:m + n;
- 空间:1;
搜索二维矩阵 2
题目
- 240;
思路
- 二分查找;
- 对每行进行二分查找即可;
- 双指针;
- 从右上角搜索元素;
- 若 matrix[row,col] === target,返回 true;
- 若 matrix[row,col] > target,因为列升序,所以 col 列全部大于 target,col--;
- 若 matrix[row,col] < target,因为行升序,所以 row 列全部大于 target,row++;
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
var searchMatrix = function (matrix, target) {
const rows = matrix.length;
const cols = matrix[0].length;
let row = 0;
let col = cols - 1;
while (row < rows && col >= 0) {
const current = matrix[row][col];
if (target === current) return true;
if (target < current) {
col--;
} else {
row++;
}
}
return false;
};
复杂度
- 时间:m + n;
- 空间:1;
x 的平方根
问题
- 69;
思路
- 基于二分,从 0 到 x 遍历,找到
k^2<=x的最大结果; - 循环中可能无法 return,所以最后结果需要判断是否向下取整;
/**
* @param {number} x
* @return {number}
*/
var mySqrt = function (x) {
let left = 0;
let right = x;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
const value = mid * mid;
if (value === x) return mid;
else if (value > x) right = mid;
else left = mid + 1;
}
if (left * left > x) return left - 1;
else return left;
};
复杂度
- 时间:logn;
- 空间:1;
寻找重复数
题目
- 287;
思路
- 定义首尾指针;
- 计算 nums[mid],统计 num 中小于等于 mid 的数量 count;
- 如果
count <= mid,重复元素其值不可能在 [1,mid] 中,left=mid+1;- 因为 [1,mid] 有 mid 个不重复的数,如果重复元素在 [1,mid] 中 count 必然大于 mid;
- 反之 right = mid;
- 如果
/**
* @param {number[]} nums
* @return {number}
*/
var findDuplicate = function (nums) {
let left = 0;
let right = nums.length - 1;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
let count = 0;
for (const num of nums) {
if (num <= mid) count++;
}
if (count <= mid) left = mid + 1;
else right = mid;
}
return left;
};
复杂度
- 时间:nlogn;
- 空间:1;
最长递增子序列
题目
- 300;
思路
- 我不知道原理,死记硬背吧。。。
- 维护一个单调递减栈;
- 遍历数组,如果数组大于栈顶,直接添加;
- 反之覆盖掉比他大的第一个元素,使用二分查找降低复杂度;
/**
* @param {number[]} nums
* @return {number}
*/
var lengthOfLIS = function (nums) {
const minStack = [nums[0]];
for (let i = 1; i < nums.length; i++) {
const num = nums[i];
if (num > minStack[minStack.length - 1]) {
minStack.push(num);
} else {
let left = 0;
let right = minStack.length;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
if (num < minStack[mid]) right = mid;
else if (num === minStack[mid]) right = mid;
else if (num > minStack[mid]) left = mid + 1;
}
minStack[left] = num;
}
}
return minStack.length;
};
复杂度
- 时间:nlogn;
- 空间:n;
数据流的中位数
题目
- 295;
思路
- 使用二分查找找到第一个大于其的位置;
- 堆;
- 维护一个小顶堆 A 和大顶堆 B;
- A 维护较大的一半,B 维护较小的一半;
- 添加元素;
- 若 A.length === B.length,向 A 添加;
- 首先向 B 添加,然后向 A 添加 B 的堆顶;
- 反之向 B 添加;
- 首先向 A 添加,然后向 B 添加 A 的堆顶;
- 若 A.length === B.length,向 A 添加;
- 返回元素;
- 若 A.length === B.length,返回 A 和 B 的堆顶的平均数;
- 反之返回 A 的堆顶;
var MedianFinder = function () {
this.arr = [];
};
/**
* @param {number} num
* @return {void}
*/
MedianFinder.prototype.addNum = function (num) {
let left = 0;
let right = this.arr.length;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
if (this.arr[mid] === num) right = mid;
else if (this.arr[mid] > num) right = mid;
else left = mid + 1;
}
this.arr.splice(left, 0, num);
};
/**
* @return {number}
*/
MedianFinder.prototype.findMedian = function () {
const mid = Math.floor((this.arr.length - 1) / 2);
if (this.arr.length % 2 === 1) {
return this.arr[mid];
} else {
return (this.arr[mid] + this.arr[mid + 1]) / 2;
}
};
/**
* Your MedianFinder object will be instantiated and called as such:
* var obj = new MedianFinder()
* obj.addNum(num)
* var param_2 = obj.findMedian()
*/
双指针法
基础
对撞指针
基本概念
- 使用两个指针 left,right,指向数组两端;
- left 不断递增,right 不断递减,直至两个指针碰撞;
left, right = 0, len(nums) - 1
while left < right:
if 满足要求的特殊条件:
return 符合条件的值
elif 一定条件 1:
left += 1
elif 一定条件 2:
right -= 1
return 没找到 或 找到对应值
适用范围
- 查找有序数组中某约束条件的元素问题;
- 字符串反转问题;
快慢指针
基本概念
- 使用快慢指针 slow,fast;
- slow 指向第一个元素;
- fast 指向第二个元素;
- 根据不同的条件移动不同的指针;
- 根据不同条件跳出循环;
- 快指针移动至数组末端;
- 两指针相交;
- 其他条件。。。
slow = 0
fast = 1
while 没有遍历完:
if 满足要求的特殊条件:
slow += 1
fast += 1
return 合适的值
适用范围
- 数组的移动,删除问题;
- 链表是否有环,长度问题;
分离指针
基本概念
- 两个指针属于不同的数组;
- 使用两个指针 left1,left2;
- 根据不同的条件移动不同的指针;
- 一个数组遍历完,或其他特殊条件跳出循环体;
left_1 = 0
left_2 = 0
while left_1 < len(nums1) and left_2 < len(nums2):
if 一定条件 1:
left_1 += 1
left_2 += 1
elif 一定条件 2:
left_1 += 1
elif 一定条件 3:
left_2 += 1
适用范围
- 有序数组的合并,交集,并集问题;
双指针题目
两数之和 - 输入有序数组
题目
- 167;
思路
- 使用数组两端指针 left,right;
- 判断对应元素之和与 target 关系;
- 等于 target,返回结果;
- 大于 target,right -= 1;
- 小于 target,left += 1;
/**
* @param {number[]} numbers
* @param {number} target
* @return {number[]}
*/
var twoSum = function (numbers, target) {
let left = 0;
let right = numbers.length;
while (left < right) {
const sum = numbers[left] + numbers[right];
if (sum === target) return [left + 1, right + 1];
else if (sum < target) left++;
else right--;
}
return [-1, -1];
};
复杂度
- 时间:n;
- 空间:1;
三数之和
问题
- 15;
思路
- 首先对数组进行排序,便于去重;
- 遍历数组,当前位置为 a;
- 使用对撞指针 left,right;
- left 指向 a + 1,right 指向数组末尾;
- 如果 nums[a] === nums[a-1],continue;
- 判断三元组;
- 如果 nums[a] + nums[left] + nums[right] === 0,添加三元组;
- 如果 nums[left] === nums[left+1],left++
- right 同理,right--;
- 若 > 0,right--;
- 若 < 0,left++;
- 如果 nums[a] + nums[left] + nums[right] === 0,添加三元组;
- 使用对撞指针 left,right;
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function (nums) {
nums = nums.sort((a, b) => a - b);
const res = [];
for (let i = 0; i < nums.length; i++) {
if (i > 0 && nums[i - 1] === nums[i]) continue;
let j = i + 1;
let k = nums.length - 1;
while (j < k) {
const sum = nums[i] + nums[j] + nums[k];
if (sum === 0) {
res.push([nums[i], nums[j], nums[k]]);
while (j < k && nums[j] === nums[j + 1]) {
j++;
}
while (j < k && nums[k] === nums[k - 1]) {
k--;
}
j++;
k--;
} else if (sum < 0) {
j++;
} else {
k--;
}
}
}
return res;
};
复杂度
- 时间:n^2;
- 空间:n;
最接近的三数之和
题目
- 16;
思路
- 同三数之和,只是将结果变为 sum 和 target 的差值;
- 不需要去重;
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var threeSumClosest = function (nums, target) {
nums = nums.sort((a, b) => a - b);
let res = Infinity;
for (let i = 0; i < nums.length; i++) {
let j = i + 1;
let k = nums.length - 1;
while (j < k) {
const sum = nums[i] + nums[j] + nums[k];
if (Math.abs(target - res) > Math.abs(target - sum)) res = sum;
if (sum === target) {
return res;
} else if (sum < target) {
j++;
} else {
k--;
}
}
}
return res;
};
复杂度
- 时间:n^2;
- 空间:n;
验证回文串
问题
- 125;
思路
- 给定 s 两端指针 left,right;
- 判断 left 和 right 是否相等;
- 相等,left++,right--;
- 不相等,返回 false;
- 若 left === right,跳出循环;
/**
* @param {string} s
* @return {boolean}
*/
var isPalindrome = function (s) {
s = s.toLowerCase().replace(/[^0-9a-z]/g, "");
let left = 0;
let right = s.length - 1;
while (left < right) {
if (s[left] !== s[right]) return false;
left++;
right--;
}
return true;
};
复杂度
- 时间/空间:s.length;
盛最多水的容器
问题
- 11;
思路
- 给定 height 两端指针 left,right;
- 容器有两个隔板构成,定义状态为两个隔板的索引
[left,right]; - 容器容量为
cap[i,j] = min(ht[left],ht[right]) * (left-right); - 假设较短板为 left,只有 left 向 right 靠近时,容器容量可能增大,同时更新 cap;
- 直至 left,right,返回最大 cap;
/**
* @param {number[]} height
* @return {number}
*/
var maxArea = function (height) {
let left = 0;
let right = height.length - 1;
let cap = 0;
while (left < right) {
cap = Math.max(cap, Math.min(height[left], height[right]) * (right - left));
if (height[right] > height[left]) left++;
else right--;
}
return cap;
};
复杂度
- 时间:n;
- 空间:1;
删除有序数组重复项
问题
- 26;
思路
- 定义快慢指针 slow,fast;
- slow 指向去重数组后的末尾位置;
- fast 指向当前元素;
- slow = 0,fast = 1;
- 判断 nums[slow] 和 nums[fast] 是否相等;
- 不相等,slow++,nums[slow] = nums[fast];
- fast++;
- 重复以上两步,直至 fast = nums.length;
/**
* @param {number[]} nums
* @return {number}
*/
var removeDuplicates = function (nums) {
let slow = 0;
let fast = 1;
while (fast < nums.length) {
if (nums[slow] !== nums[fast]) {
slow++;
nums[slow] = nums[fast];
}
fast++;
}
return slow + 1;
};
复杂度
- 时间:n;
- 空间:1;
移除元素
题目
- 27;
思路
- 同删除有序数组重复项;
/**
* @param {number[]} nums
* @param {number} val
* @return {number}
*/
var removeElement = function (nums, val) {
let left = 0;
let right = 0;
while (right < nums.length) {
if (nums[right] !== val) nums[left++] = nums[right];
right++;
}
return left;
};
复杂度
- 时间:n;
- 空间:1;
移动零
问题
- 283;
思路
- 使用快慢指针,slow 指向非零数组末端,fast 指向当前元素,两者初始均为 0;
- 不断右移 fast,如果 nums[fast] 非零,交换 nums[fast] 和 nums[slow],slow++;
- fast 移动至数组末端,slow 其后所有元素均为 0;
/**
* @param {number[]} nums
* @return {void} Do not return anything, modify nums in-place instead.
*/
var moveZeroes = function (nums) {
let slow = 0;
let fast = 0;
while (fast < nums.length) {
if (nums[fast] !== 0) {
[nums[slow], nums[fast]] = [nums[fast], nums[slow]];
slow++;
}
fast++;
}
};
复杂度
- 空间:n;
- 时间:1;
训练计划 1
题目
思路
- 使用快慢指针,slow 指向奇数数组末端,fast 指向当前元素,两者初始均为 0;
- 不断右移 fast,如果 nums[fast] 非偶,交换 nums[fast] 和 nums[slow],slow++;
- fast 移动至数组末端,slow 其后所有元素均为 0;
/**
* @param {number[]} actions
* @return {number[]}
*/
var trainingPlan = function (actions) {
let left = 0;
let right = 0;
while (right < actions.length) {
if (actions[right] % 2 === 1) {
[actions[left], actions[right]] = [actions[right], actions[left]];
left++;
}
right++;
}
return actions;
};
复杂度
- 空间:n;
- 时间:1;
合并两个有序数组
题目
- 88;
思路
- 基于快慢指针;
- index1,index2 分别指向 nums1,nums2 尾部;
- index 指向 nums1 尾部;
- 比较
nums1[index1]和nums2[index2]大小,较大值存入 nums1,然后向前继续遍历; - 若 num 剩余元素;
- nums2:将 nums2 剩余元素一一赋值;
- nums1:剩余元素即最后结果位置,不用移动;
/**
* @param {number[]} nums1
* @param {number} m
* @param {number[]} nums2
* @param {number} n
* @return {void} Do not return anything, modify nums1 in-place instead.
*/
var merge = function (nums1, m, nums2, n) {
let i = m - 1;
let j = n - 1;
let k = m + n - 1;
while (i >= 0 && j >= 0) {
if (nums1[i] > nums2[j]) {
nums1[k--] = nums1[i--];
} else {
nums1[k--] = nums2[j--];
}
}
while (j >= 0) {
nums1[k--] = nums2[j--];
}
};
复杂度
- 时间/空间:m + n;
求两个数组交集
题目
- 349;
思路
- 排序 nums1,nums2;
- 使用分离指针 i,j,分别指向两个数组;
- 如果 nums[i] === nums[j],加入答案数组,两者右移;
- 如果 nums[i] > nums[j],j++;
- 如果 nums[i] < nums[j],i++;
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number[]}
*/
var intersection = function (nums1, nums2) {
nums1.sort((a, b) => a - b);
nums2.sort((a, b) => a - b);
let i = 0;
let j = 0;
const res = new Set();
while (i < nums1.length && j < nums2.length) {
if (nums1[i] === nums2[j]) {
res.add(nums1[i]);
i++;
j++;
} else if (nums1[i] > nums2[j]) j++;
else i++;
}
return [...res];
};
复杂度
- 时间:n;
- 空间:1;
字符串相加
问题
- 415;
思路
- 使用字符串模拟加法运算;
- 字符串使用数组形式存储,一位对应一个数;
- 判断两者数组长度,超出位数者,使用前导零补充;
- 使用分离指针,指向两个数组末端;
- 使用 carry 表示是否进位;
/**
* @param {string} num1
* @param {string} num2
* @return {string}
*/
var addStrings = function (num1, num2) {
let right1 = num1.length - 1;
let right2 = num2.length - 1;
const sum = [];
let carry = 0;
while (carry || right1 >= 0 || right2 >= 0) {
const value1 = right1 >= 0 ? Number(num1[right1]) : 0;
const value2 = right2 >= 0 ? Number(num2[right2]) : 0;
right1--;
right2--;
let value = value1 + value2 + carry;
if (value >= 10) {
value %= 10;
carry = 1;
} else {
carry = 0;
}
sum.unshift(value);
}
return sum.join("");
};
复杂度
- 时间/空间:max(len(nums1),len(nums2));
36 进制加减法
题目
- 36 进制由 0-9,a-z,共 36 个字符表示,要求按照加法规则计算出任意两个 36 进制正整数的和,如 1b + 2x = 48;
思路
- 思路同两数相加;
- 定义 getInt 和 getChar 两个函数进行十进制和 36 进制的转换;
const offset = "a".charCodeAt(0) - 10;
const getInt = (ch) => {
if (ch >= "0" && ch <= "9") {
return Number(ch);
} else {
return ch.charCodeAt(0) - offset;
}
};
const getChar = (num) => {
if (num >= 0 && num <= 9) {
return String(num);
} else {
return String.fromCharCode(num + offset);
}
};
var addStrings = function (num1, num2) {
let right1 = num1.length - 1;
let right2 = num2.length - 1;
const sum = [];
let carry = 0;
while (carry || right1 >= 0 || right2 >= 0) {
const value1 = right1 >= 0 ? getInt(num1[right1]) : 0;
const value2 = right2 >= 0 ? getInt(num2[right2]) : 0;
right1--;
right2--;
let value = value1 + value2 + carry;
if (value >= 36) {
value %= 36;
carry = 1;
} else {
carry = 0;
}
sum.unshift(getChar(value));
}
return sum.join("");
};
console.log(addStrings("1b", "2x")); // 48
复杂度
- 时间:n;
- 空间:n;
下一个排列
题目
- 31;
思路
- 基本思想;
- 低位寻找较大的数字,替换前面较小的数字;
- 变大幅度尽量的小;
- 实现步骤;
- 从右向左寻找第一个比右邻居小的元素 nums[i];
- nums[i+1,-1] 必然是降序排列;
- 从右向左寻找第一个大于 nums[i] 的元素 nums[j],交换两者;
- 倒序排列 nums[i+1,-1],使其更小;
/**
* @param {number[]} nums
* @return {void} Do not return anything, modify nums in-place instead.
*/
var nextPermutation = function (nums) {
let i = nums.length - 2;
while (i >= 0) {
if (nums[i] < nums[i + 1]) break;
i--;
}
if (i >= 0) {
let j = nums.length - 1;
while (j >= 0 && nums[j] <= nums[i]) {
j--;
}
[nums[i], nums[j]] = [nums[j], nums[i]];
}
let left = i + 1;
let right = nums.length - 1;
while (left < right) {
[nums[left], nums[right]] = [nums[right], nums[left]];
left++;
right--;
}
return nums;
};
复杂度
- 时间:n;
- 空间:1;
有效三角形个数
题目
- 611;
思路
- 三角形要求两边之和大于第三边;
- 首先对数组进行排序;
- 假设
a<=b<=c,如果a+b>c, a+c>b, b+c>a一定成立; - 从 i = 2 开始遍历;
- 维护有效三角形数量 res;
- 定义首尾指针,执行 0 和 i-1;
- 如果
nums[left] + nums[right] <= nums[i],left++; - 反之三角形成立,所以 [left,right) 都成立,res += right-left,同时 right--;
- 固定最大边的原理;
- 如果固定最小边,使
a+b>c成立,可能存在 b++ 或 c -- 两种情况;
- 如果固定最小边,使
/**
* @param {number[]} nums
* @return {number}
*/
var triangleNumber = function (nums) {
nums = nums.sort((a, b) => a - b);
let res = 0;
for (let i = 2; i < nums.length; i++) {
let left = 0;
let right = i - 1;
while (left < right) {
if (nums[left] + nums[right] > nums[i]) {
res += right - left;
right--;
} else {
left++;
}
}
}
return res;
};
复杂度
- 时间:n^2;
- 空间:logn;
压缩字符串
题目
- 443;
思路
- 定义快慢指针 slow,fast;
- slow 指向压缩后当前字符位置,fast 压缩前当前字符位置;
- 使用 start 记录 fast 开始的位置,过滤相同字符;
- str[slow]=str[start],slow++;
- 基于 start 和 fast 判断压缩字符数量;
- 如果为 1,不用记录;
- 如果大于 1,存入对应字符数量;
/**
* @param {character[]} chars
* @return {number}
*/
var compress = function (chars) {
let slow = 0;
let fast = 0;
while (fast < chars.length) {
const start = fast;
while (fast + 1 < chars.length && chars[fast] === chars[fast + 1]) {
fast++;
}
chars[slow] = chars[start];
slow++;
const count = fast - start + 1;
if (count > 1) {
const str = String(count);
for (const ch of str) {
chars[slow++] = ch;
}
}
fast++;
}
return slow;
};
复杂度
- 时间:n;
- 空间:1;
滑动窗口
基础
滑动窗口算法
- 数组/字符串维护一个固定长度或不定长度的窗口;
- 窗口可进行滑动操作和缩放操作;
- 是快慢指针的特殊形式;
适用范围
- 查找满足一定条件,连续区间的性质;
固定长度滑动窗口
- 使用两个指针 left,right,指向 0;
- 若窗口小于固定长度,右移 right;
- 当窗口到达固定长度,判断窗口元素是否满足题目限定条件;
- 满足,更新结果;
- 向右移动窗口;
- 重复上一步,直至 right 到达数组末尾;
left = 0
right = 0
while right < len(nums):
window.append(nums[right])
# 超过窗口大小时, 缩小窗口, 维护窗口中始终为 window_size 的长度
if right - left + 1 >= window_size:
# ... 维护答案
window.popleft()
left += 1
# 向右侧增大窗口
right += 1
不定长度滑动窗口
- 使用两个指针 left,right,指向 0;
- 不断右移 right,直至满足要求;
- 不断左移,直至满足要求;
- 重复以上两步,直至 right 到达末尾;
left = 0
right = 0
while right < len(nums):
window.append(nums[right])
while 窗口需要缩小:
# ... 可维护答案
window.popleft()
left += 1
# 向右侧增大窗口
right += 1
答案维护
- 维护 res 时;
- 可能需要在循环或条件外面进行一些情况的判断,或者更新一次 res,避免达不到条件,导致 res 错误;
滑动窗口题目
大于 K 且平均值大于阈值的子数组数目
题目
- 1343;
思路
- 使用固定长度滑动窗口,定义指针 left,right,窗口长度为 k;
- 当窗口长度为 k 时,判断窗口平均值是否大于阈值;
- 大于,则保存答案,反之不做任何处理;
/**
* @param {number[]} arr
* @param {number} k
* @param {number} threshold
* @return {number}
*/
var numOfSubarrays = function (arr, k, threshold) {
let right = 0;
let left = 0;
let ans = 0;
let sum = 0;
while (right < arr.length) {
sum += arr[right];
if (right - left + 1 === k) {
if (sum >= threshold * k) {
ans++;
}
sum -= arr[left];
left++;
}
right++;
}
return ans;
};
复杂度
- 时间/空间:n;
无重复字符的最长子串
题目
- 3;
思路
- 使用不定滑动窗口,定义 right,left = 0,0;
- 右移 right,添加右侧字符,直至出现重复字符;
- 右移 left,直至重复字符消失;
- 更新维护无重复字符的最长子串长度;
- 重复以上两步,直至 right 达到字符串末尾;
/**
* @param {string} s
* @return {number}
*/
var lengthOfLongestSubstring = function (s) {
let left = 0;
let right = 0;
let res = 0;
const map = {};
while (right < s.length) {
if (map[s[right]]) {
map[s[right]] += 1;
} else {
map[s[right]] = 1;
}
while (map[s[right]] > 1) {
map[s[left]] -= 1;
left++;
}
res = Math.max(res, right - left + 1);
right++;
}
return res;
};
复杂度
- 时间:n;
- 空间:字符集大小;
长度最小的子数组
问题
- 209;
思路
- 使用不定长度滑动窗口,定义指针 left,right = 0;
- 右移 right,直至 sum > target;
- 右移 left,直至 sum < target;
- 维护更新最小长度 min;
- 重复以上操作,直至 right 到达数组末尾;
/**
* @param {number} target
* @param {number[]} nums
* @return {number}
*/
var minSubArrayLen = function (target, nums) {
let left = 0;
let right = 0;
let sum = 0;
let res = nums.length + 1;
while (right < nums.length) {
sum += nums[right];
while (sum >= target) {
res = Math.min(res, right - left + 1);
sum -= nums[left];
left++;
}
right++;
}
return res === nums.length + 1 ? 0 : res;
};
复杂度
- 时间:n;
- 空间:1;
乘积小于 k 的子数组
问题
- 713;
思路
- 使用不定长度滑动窗口,定义指针 left,right = 0;
- 右移 right,直至 dot > target;
- 右移 left,直至 dot < target;
- 维护更新子数组个数 count,子数组个数为 right-left+1;
- 重复以上操作,直至 right 到达数组末尾;
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var numSubarrayProductLessThanK = function (nums, k) {
if (k <= 1) return 0;
let left = 0;
let right = 0;
let dot = 1;
let res = 0;
while (right < nums.length) {
dot *= nums[right];
while (dot >= k) {
dot /= nums[left];
left++;
}
res += right - left + 1;
right++;
}
return res;
};
复杂度
- 时间:n;
- 空间:1;
最小覆盖子串
问题
- 76;
思路
- 使用不定长度滑动窗口;
- 定义 left,right = 0;
- 最小字符串起始位置 start,最小字符串长度 min;
- 记录 t 缺失的字符极其数量 need;
- 记录当前缺失字符数种类 miss;
- 右移 right,直至 miss ===0;
- 右移 left,直至 miss !== 0;
- 重复以上操作,直至 right 到达数组末尾;
/**
* @param {string} s
* @param {string} t
* @return {string}
*/
var minWindow = function (s, t) {
let left = 0;
let right = 0;
let start = s.length;
let min = s.length + 1;
let need = {};
let miss = 0;
for (const str of t) {
if (need[str]) {
need[str] += 1;
} else {
need[str] = 1;
miss++;
}
}
while (right < s.length) {
if (need[s[right]] != null) {
need[s[right]]--;
}
if (need[s[right]] === 0) {
miss--;
}
while (miss === 0) {
if (right - left + 1 < min) {
start = left;
min = right - left + 1;
}
if (need[s[left]] != null) {
need[s[left]]++;
}
if (need[s[left]] > 0) miss++;
left++;
}
right++;
}
return s.slice(start, start + min);
};
复杂度
- 时间:n;
- 空间:s 和 t 的字符集大小;
最大连续 1 的个数 3
题目
- 1004;
思路
- 定义不定长度滑动窗口 left 和 right;
- 定义 maxCount 维护包含 1 的最长连续子数组长度,zero 维护窗口内 0 的个数;
- zero>k,left 左移直至
zero <= k,同时维护 maxCount; - 最后返回 maxCount;
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var longestOnes = function (nums, k) {
let left = 0;
let right = 0;
let max = 0;
let zero = 0;
while (right < nums.length) {
if (nums[right] === 0) zero++;
while (zero > k) {
if (nums[left] === 0) zero--;
left++;
}
max = Math.max(max, right - left + 1);
right++;
}
return max;
};
复杂度
- 时间:n;
- 空间:1;
前缀和
- 前缀和:num[0:i]的和;
- 定义前缀和数组 prefixSum[i]=nums[0]+。。。+nums[i];
- 数组某项 = 相邻前缀和之差:nums[i]=prefixSum[i]-prefixSum[i-1];
- nums[i:j]的和:prefixSum[j]-prefixSum[i-1];
- 移除边界的条件的前缀和:num 前 i 项的和;
- 定义前缀和数组 prefixSum[i]=nums[0]+。。。+nums[i-1];
- 数组某项 = 相邻前缀和之差:nums[i]=prefixSum[i+1]-prefixSum[i];
- nums[i:j]的和:prefixSum[j+1]-prefixSum[i];
前缀和题目
和为 K 的子数组
题目
- 560;
思路
- 基于前缀和思想;
- 题目转换;
- 有多少种 i,j 组合,使得 nums[i:j] 和为 k;
- 即 prefixSum[j+1]-prefixSum[i] = k;
- 暴力解法:双重循环前缀和;
- 空间优化:基于两数之和思想;
- 手动添加 [0:1] 适配边界条件;
- 遍历数组,求前缀和,将 [sum,count] 存入 Map 或递增 count;
- 如果 Map 存在[当前前缀和-k],count+=Map[当前前缀和-k];
- 返回 count;
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var subarraySum = function (nums, k) {
const map = {
0: 1,
};
let res = 0;
let sum = 0;
for (const num of nums) {
sum += num;
if (map[sum - k]) {
res += map[sum - k];
}
if (map[sum]) map[sum]++;
else map[sum] = 1;
}
return res;
};
复杂度
- 时间:n;
- 空间:n;
和至少为 K 的最短子数组
题目
- 862;
思路
- 计算前缀和;
- 暴力计算会超时,使用单调栈优化;
- 第一层优化;
- 如果 prefixSum[i] - prefixSum[minStack[0]] >= k;
- 无论 i 后面的 prefixSum 大还是小,都不可能得到比 i - minStack[0] 更小的值;
- 此时为最短值,维护 res,并把 minStack[0] 移除;
- 第二层优化;
- 如果 prefixSum[i] < prefixSum[minStack.at(-1)];
- 若后续存在 x - prefixSum[minStack.at(-1)] >= k;
- 必然 x - prefixSum[i] >= k,此长度更短,因此移除 prefixSum[minStack.at(-1)];
- 第一层优化;
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var shortestSubarray = function (nums, k) {
const n = nums.length;
const prefixSum = new Array(n + 1);
prefixSum[0] = 0;
for (let i = 1; i <= n; i++) {
prefixSum[i] = prefixSum[i - 1] + nums[i - 1];
}
let res = n + 1;
const minStack = [];
for (let i = 0; i <= n; i++) {
while (
minStack.length !== 0 &&
prefixSum[i] - prefixSum[minStack[0]] >= k
) {
const index = minStack.shift();
res = Math.min(i - index, res);
}
while (minStack.length !== 0 && prefixSum[i] < prefixSum[minStack.at(-1)]) {
minStack.pop();
}
minStack.push(i);
}
return res === n + 1 ? -1 : res;
};
复杂度
- 时间:n^2;
- 空间:n;