树
二叉树
基础
二叉树
- 非线性数据结构;
- 最多两个子节点,依次为左子节点和右子节点;
- 对应的树称为左子树和右子树;
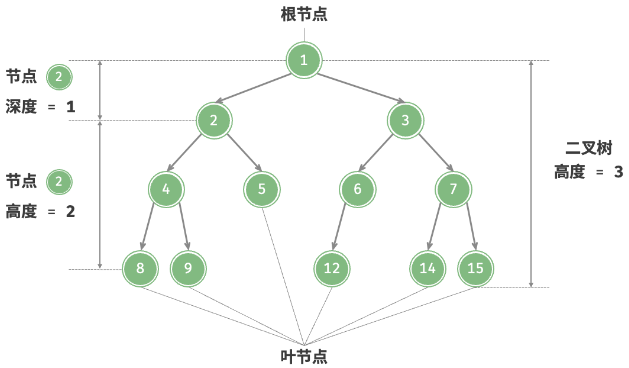
常见术语
- 根节点:树的顶部节点;
- 叶节点:没有子节点的节点;
- 层:从顶到底递增,根节点为 1;
- 度:节点的子节点数量;
- 边:连接两个节点的线段;
- 高度:该节点到最远节点的边的数量;
- 深度:根节点到该节点的边的数量;
常见二叉树类型
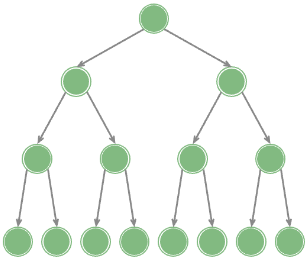
完美二叉树
- 所有层的节点被填满;
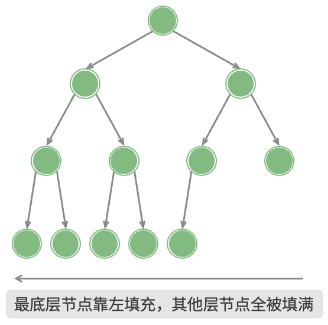
完全二叉树
- 只有最底层的节点没有填满;
- 最底层节点向左靠;
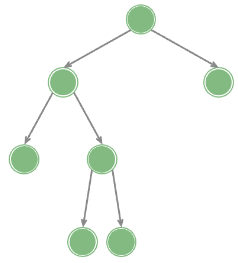
完满二叉树
- 除叶节点之外的节点都有两个子节点;
平衡二叉树
- 左子树和右子树高度之差不超过 1;

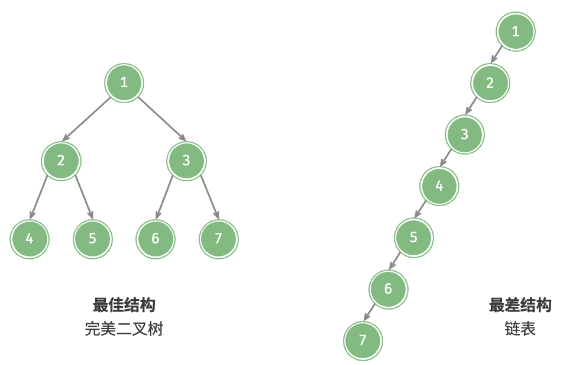
二叉树的退化
二叉树的退化
- 所有节点偏向一侧,退化为链表;
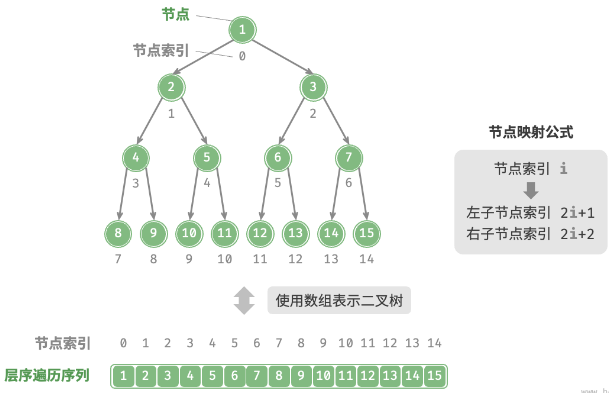
二叉树数组表示
完美二叉树
任意二叉树
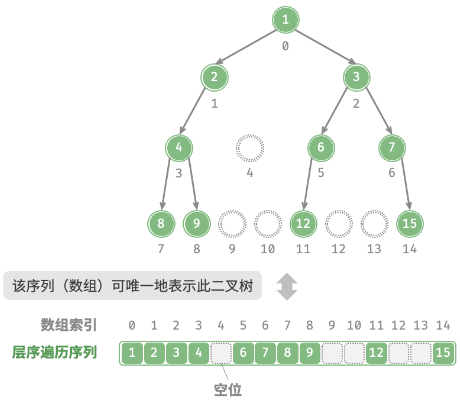
优点
- 遍历,访问速度快;
- 允许随机访问;
缺点
- 不适合存储过大的树;
- 插入和删除效率低;
- 存在大量空节点时,空间利用率低;
二叉树计算公式
二叉树查找路径
- 不管他是前序中序还是后序;
- 按照他的排序建树即可,判断二叉树是否有效;
节点公式
- 叶子节点数:叶子节点数 = 度为 2 的节点数 + 1,度为 1 的节点数量未知;
- 节点总数;
- 总数最多 2^k-1;
- 每层最多 2^(k-1);
- 最小深度:
log_2^{N+1};
二叉树遍历
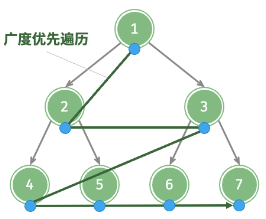
层序遍历
- 逐层访问;
- 广度优先遍历;
- 时间复杂度为 O(n);
- 空间复杂度为 O(n);
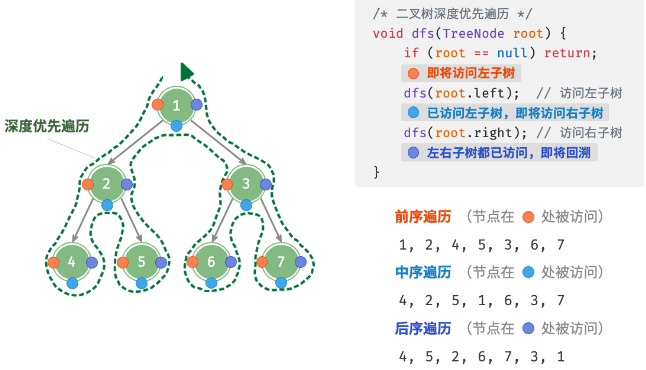
前序, 中序, 后序遍历
概述
- 深度优先遍历;
- 根据根节点的访问顺序,分为前序,中序和后序;
- 时间复杂度为 O(n);
- 空间复杂度为 O(n);
遍历顺序
- 前序:根节点 - 左子树 - 右子树;
- 中序:左子树 - 根节点 - 右子树;
- 后序:左子树 - 右子树 - 根节点;
模板代码
var traversal = function (root) {
if (root == null) return [];
const res = [];
const stack = [];
let node = root;
while (node || stack.length! == 0) {
while (node != null) {
stack.push(node);
node = node.left;
}
node = stack.pop();
node = node.right;
}
return res;
};
二叉树遍历题目
二叉树前序遍历
题目
- 144;
思路
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var preorderTraversal = function (root) {
if (root == null) return [];
const res = [];
const preorder = (node) => {
res.push(node.val);
if (node.left != null) {
preorder(node.left);
}
if (node.right != null) {
preorder(node.right);
}
};
preorder(root);
return res;
};
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var preorderTraversal = function (root) {
const res = [];
const stack = [];
let node = root;
while (node || stack.length! == 0) {
while (node != null) {
res.push(node.val);
stack.push(node);
node = node.left;
}
node = stack.pop();
node = node.right;
}
return res;
};
二叉树的中序遍历
题目
- 94;
思路
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var inorderTraversal = function (root) {
if (root == null) return [];
const res = [];
const preorder = (node) => {
if (node.left != null) {
preorder(node.left);
}
res.push(node.val);
if (node.right != null) {
preorder(node.right);
}
};
preorder(root);
return res;
};
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var preorderTraversal = function (root) {
const res = [];
const stack = [];
let node = root;
while (node || stack.length! == 0) {
while (node != null) {
stack.push(node);
node = node.left;
}
node = stack.pop();
res.push(node.val);
node = node.right;
}
return res;
};
二叉树的后序遍历
题目
- 145;
思路
- 前序遍历:中 - 左 - 右;
- 后序遍历:左 - 右 - 中;
- 基于前序遍历,遍历 "中 - 右 - 左";
- 最后将结果倒序即后序遍历;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var postorderTraversal = function (root) {
if (root == null) return [];
const res = [];
const preorder = (node) => {
if (node.left != null) {
preorder(node.left);
}
if (node.right != null) {
preorder(node.right);
}
res.push(node.val);
};
preorder(root);
return res;
};
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var postorderTraversal = function (root) {
const res = [];
const stack = [];
let cur = root;
while (stack.length !== 0 || cur != null) {
while (cur != null) {
res.push(cur.val);
stack.push(cur);
cur = cur.right;
}
cur = stack.pop();
cur = cur.left;
}
return res.reverse();
};
二叉树的层序遍历
题目
- 102;
思路
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var levelOrder = function (root) {
if (root == null) return [];
const res = [];
const queue = [root];
while (queue.length !== 0) {
let size = queue.length;
const level = [];
while (size > 0) {
const node = queue.shift();
level.push(node.val);
if (node.left != null) {
queue.push(node.left);
}
if (node.right != null) {
queue.push(node.right);
}
size--;
}
level.length !== 0 && res.push(level);
}
return res;
};
复杂度
- 时间:n;
- 空间:n;
二叉树的锯齿形层序遍历
题目
- 103;
思路
- 设置表示为 odd 表示是奇数层还是偶数层;
- 奇数层 level 队尾添加,偶数层队尾添加;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var zigzagLevelOrder = function (root) {
if (root == null) return [];
const res = [];
const queue = [root];
let odd = true;
while (queue.length > 0) {
const level = [];
const size = queue.length;
for (let i = 0; i < size; i++) {
const node = queue.shift();
if (odd) {
level.push(node.val);
} else {
level.unshift(node.val);
}
if (node.left != null) {
queue.push(node.left);
}
if (node.right != null) {
queue.push(node.right);
}
}
res.push(level);
odd = !odd;
}
return res;
};
复杂度
- 时间:n;
- 空间:n;
二叉树的最近公共祖先
题目
- 236;
思路
- 设 anc 为 p 和 q 的最近公共祖先;
- p 和 q 分别在 anc 的左右子树;
- p 或 q 为 anc,q 或 p 在 anc 的子树;
- 递归思路;
- 从 root 开始递归;
- 如果 cur 为 none,cur 不可能为最近公共祖先,返回 null;
- 如果 cur 为 p 或 q,直接返回 cur;
- 如果 cur 不为 null,递归遍历左右子树;
- 若左右子树结果不为空,p 和 q 分别在左右子树,返回 cur;
- 如果左子树为空,说明 p 和 q 都在 右子树,返回右子树,右子树同理;
- 如果都为空,返回 none;
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
var lowestCommonAncestor = function (root, p, q) {
const dfs = (node) => {
if (node == null) return null;
if (node === p || node === q) return node;
const left = dfs(node.left);
const right = dfs(node.right);
if (left != null && right != null) return node;
if (left != null) return left;
if (right != null) return right;
return null;
};
return dfs(root);
};
复杂度
- 时间:n;
- 空间:n;
二叉树的最大深度
题目
- 104;
思路
- curHeight = max(leftHeight,rightHeight) + 1;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function (root) {
const traversal = (cur) => {
if (cur == null) return 0;
const left = traversal(cur.left);
const right = traversal(cur.right);
const res = Math.max(left, right) + 1;
return res;
};
const res = traversal(root);
return res;
};
复杂度
- 时间:n;
- 空间:n;
二叉树的最小深度
题目
- 111;
思路
- 与二叉树的最大深度不同,需要考虑子树是否为空的情况;
- 如果节点为空,返回 0;
- 如果左右子树为空,说明为叶子结点,返回 1;
- 计算左右子树的高度,判断子树是否存在;
- 将非空子树的较小深度+1 作为当前节点的最小叶子节点深度;
- 这就是和最大深度的区别,最大深度不用考虑子树是否为空;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function (root) {
const dfs = (node) => {
if (node == null) return 0;
if (node.left == null && node.right == null) return 1;
const left = dfs(node.left);
const right = dfs(node.right);
let min = Infinity;
if (node.left) min = Math.min(min, left);
if (node.right) min = Math.min(min, right);
return min + 1;
};
return dfs(root);
};
复杂度
- 时间:n;
- 空间:n;
路径总和 1
题目
- 112;
思路
- 定义递归函数,传入当前节点 node,目标值 target;
- 如果当前节点为空,返回 false;
- 反之 target -= node.val;
- 如果为叶子节点,比较 target === 0;
- 反之递归遍历左右子树;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {boolean}
*/
var hasPathSum = function (root, targetSum) {
let res = false;
const backtrack = (state, node, targetSum) => {
if (node.left == null && node.right == null) {
if (state === targetSum) res = true;
return;
}
if (node.left != null) {
backtrack(state + node.left.val, node.left, targetSum);
}
if (node.right != null) {
backtrack(state + node.right.val, node.right, targetSum);
}
};
if (root == null) return false;
backtrack(root.val, root, targetSum);
return res;
};
复杂度
- 时间:n;
- 空间:n;
路径总和 2
题目
- 113;
思路
- 在路径总和 1 的基础上,维护当前路径 path;
- 进入节点,添加当前节点至 path;
- 回退节点,从 path 删除当前节点;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {number[][]}
*/
var pathSum = function (root, targetSum) {
const backtrace = (res, state, node, target) => {
if (node.left == null && node.right == null) {
if (target === 0) res.push([...state]);
return;
}
if (node.left != null) {
state.push(node.left.val);
backtrace(res, state, node.left, target - node.left.val);
state.pop();
}
if (node.right != null) {
state.push(node.right.val);
backtrace(res, state, node.right, target - node.right.val);
state.pop();
}
};
if (root == null) return [];
const res = [];
backtrace(res, [root.val], root, targetSum - root.val);
return res;
};
复杂度
- 时间:n^2;
- 空间:n;
对称二叉树
题目
- 101;
思路
- 若二叉树对称;
- 左右子树内侧节点相等;
- 左右子树外侧节点相等;
- 遍历思路;
- 根节点为 null,返回 true;
- 反之递归遍历左右子树;
- 子树皆为 null,返回 true;
- 只有一个为 null,返回 false;
- 子树节点值不同,返回 false;
- 子树节点值相同;
- 递归遍历子树外侧节点是否相同;
- 递归遍历子树内侧节点是否相同;
- 层序遍历思路;
- 如果存在子树,queue 添加子树,反之添加 null;
- 判断 cur 是否为 null;
- null:level.push(null);
- 反之 level.push(node.val);
- 人为创建完全二叉树,缺失值赋值为 null;
- 检查每一层正序倒序是否一致;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isSymmetric = function (root) {
const dfs = (left, right) => {
if (left == null && right == null) return true;
if (left == null || right == null) return false;
if (left.val !== right.val) return false;
return dfs(left.left, right.right) && dfs(left.right, right.left);
};
if (root == null) return true;
return dfs(root.left, root.right);
};
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isSymmetric = function (root) {
if (root == null) return [];
const queue = [root];
while (queue.length !== 0) {
let size = queue.length;
const level = [];
while (size > 0) {
size--;
const node = queue.shift();
if (node == null) {
level.push(null);
continue;
} else {
level.push(node.val);
}
if (node.left != null) {
queue.push(node.left);
} else {
queue.push(null);
}
if (node.right != null) {
queue.push(node.right);
} else {
queue.push(null);
}
}
let left = 0;
let right = level.length - 1;
while (left < right) {
if (level[left] !== level[right]) {
return false;
}
left++;
right--;
}
}
return true;
};
复杂度
- 时间:n;
- 空间:n;
二叉树的最大路径和
题目
- 124;
思路
- 路径和;
- 经过根节点 = 左子树贡献值 + 右子树贡献值 + 根节点节点值;
- 不经过根节点 = 子树最大路径和;
- 最大路径和 = max(左子树贡献值 + 右子树贡献值 + 根节点节点值,所有子树的最大路径和);
- 定义递归函数;
- 传入当前子树根节点,计算经过该节点的子树贡献值;
- 根节点为空,贡献值为 0;
- 递归计算子树贡献值,若贡献值小于 0,返回 0;
- 返回子树的最大贡献值 + 当前子树根节点值;
- 维护最大路径和 ans;
- 传入当前子树根节点,计算经过该节点的子树贡献值;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxPathSum = function (root) {
let res = -Infinity;
const dfs = (node) => {
if (node == null) return 0;
const left = Math.max(dfs(node.left), 0);
const right = Math.max(dfs(node.right), 0);
const sum = left + right + node.val;
res = Math.max(res, sum);
return node.val + Math.max(left, right);
};
dfs(root);
return res;
};
复杂度
- 时间:n;
- 空间:n;
二叉树的右视图
题目
- 199;
思路
- 层序遍历二叉树;
- 每一层级返回最后一个节点;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var rightSideView = function (root) {
if (root == null) return [];
const queue = [root];
const res = [];
while (queue.length !== 0) {
res.push(queue[queue.length - 1].val);
const size = queue.length;
for (let i = 0; i < size; i++) {
const node = queue.shift();
if (node.left != null) {
queue.push(node.left);
}
if (node.right != null) {
queue.push(node.right);
}
}
}
return res;
};
复杂度
- 时间:n;
- 空间:n;
翻转二叉树
题目
- 226;
思路
- 基于递归 + 深度优先遍历;
- 递归翻转左右子树;
- 交换左右子树位置;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var invertTree = function (root) {
const dfs = (node) => {
if (node == null) return null;
node.left = dfs(node.left);
node.right = dfs(node.right);
[node.left, node.right] = [node.right, node.left];
return node;
};
const res = dfs(root);
return res;
};
复杂度
- 时间:n;
- 空间:n;
相同的树
题目
- 100;
思路
- 首先判断根节点是否相同;
- 其次判断两个子树是否相同;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} p
* @param {TreeNode} q
* @return {boolean}
*/
var isSameTree = function (p, q) {
const dfs = (p, q) => {
if (p == null && q == null) return true;
if (p == null || q == null) return false;
if (p.val !== q.val) return false;
return dfs(p.left, q.left) && dfs(p.right, q.right);
};
return dfs(p, q);
};
复杂度
- 时间:n;
- 空间:n;
另一颗树的子树
题目
- 572;
思路
- 即判断 s 的子树是否是 p;
- 原理同相同的树;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {TreeNode} subRoot
* @return {boolean}
*/
var isSubtree = function (root, subRoot) {
const isSameTree = (p, q) => {
if (p == null && q == null) return true;
if (p == null || q == null) return false;
if (p.val !== q.val) return false;
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
};
const dfs = (root, sub) => {
if (root == null && sub == null) return true;
if (root == null || sub == null) return false;
return isSameTree(root, sub) || dfs(root.left, sub) || dfs(root.right, sub);
};
return dfs(root, subRoot);
};
复杂度
- 时间:mn;
- 空间:mn;
二叉树的序列化和反序列化
题目
- 297;
思路
- 基于深度优先遍历即可;
- 节点之间,隔开;
- 空节点特殊符号隔开;
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* Encodes a tree to a single string.
*
* @param {TreeNode} root
* @return {string}
*/
var serialize = function (root) {
const dfs = (node) => {
if (node == null) return "kxh";
const left = dfs(node.left);
const right = dfs(node.right);
return node.val + "," + left + "," + right;
};
return dfs(root);
};
/**
* Decodes your encoded data to tree.
*
* @param {string} data
* @return {TreeNode}
*/
var deserialize = function (data) {
const dfs = (arr) => {
const rootValue = arr.shift();
if (rootValue === "kxh") return null;
const rootNode = new TreeNode(rootValue);
rootNode.left = dfs(arr);
rootNode.right = dfs(arr);
return rootNode;
};
return dfs(data.split(","));
};
/**
* Your functions will be called as such:
* deserialize(serialize(root));
*/
复杂度
- 时间:n;
- 空间:n;
二叉树展开为链表
题目
- 114;
思路
- 最简单方法;
- 首先前序遍历;
- 然后逐数组创建即可;
- 原地修改;
- 左子树添加到右子树位置;
- 右子树添加到左子树的最右节点;
- 考虑新的右子树的根节点,重复以上过程;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {void} Do not return anything, modify root in-place instead.
*/
var flatten = function (root) {
let node = root;
while (node != null) {
if (node.left == null) {
node = node.right;
continue;
}
let rightOfLeft = node.left;
while (rightOfLeft.right != null) {
rightOfLeft = rightOfLeft.right;
}
rightOfLeft.right = node.right;
node.right = node.left;
node.left = null;
node = node.right;
}
};
复杂度
- 时间:n;
- 空间:1;
二叉树还原
构造唯一二叉树
- 中序 + (前序/后序/层序) 可构造唯一二叉树;
- 前序 + 后序可构造二叉树,但不唯一;
构造思想
- 通过前序或者后序,确定根节点值;
- 找到中序中的根节点值;
- 根据中序根节点索引,确定左右子树;
- 分别对左右子树,递归以上操作,直至节点为空;
二叉树的完全性检验
题目
- 958;
思路
- 层序遍历变种;
- 空节点依旧加入队列,如果队列遇到空节点之后,又遇到非空节点,说明不是完全二叉树;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isCompleteTree = function (root) {
if (root == null) return [];
const queue = [root];
let isEmpty = false;
while (queue.length !== 0) {
let size = queue.length;
while (size > 0) {
const node = queue.shift();
if (node == null) {
isEmpty = true;
} else {
if (isEmpty) return false;
queue.push(node.left);
queue.push(node.right);
}
size--;
}
}
return true;
};
复杂度
- 时间:n;
- 空间:n;
二叉树还原题目
从前序和中序构造二叉树
题目
- 105;
思路
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} preorder
* @param {number[]} inorder
* @return {TreeNode}
*/
var buildTree = function (preorder, inorder) {
const createTree = (preorder, inorder, n) => {
if (n === 0) return null;
const root = preorder[0];
const k = inorder.indexOf(root);
const node = new TreeNode(root, null, null);
node.left = createTree(preorder.slice(1, k + 1), inorder.slice(0, k), k);
node.right = createTree(
preorder.slice(k + 1),
inorder.slice(k + 1),
n - k - 1
);
return node;
};
const res = createTree(preorder, inorder, preorder.length);
return res;
};
复杂度
- 时间:n;
- 空间:n;
从中序和后序构造二叉树
题目
- 106;
思路
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} inorder
* @param {number[]} postorder
* @return {TreeNode}
*/
var buildTree = function (inorder, postorder) {
const createTree = (inorder, postorder, n) => {
if (n === 0) return null;
const root = postorder[postorder.length - 1];
const k = inorder.indexOf(root);
const node = new TreeNode(root, null, null);
node.left = createTree(inorder.slice(0, k), postorder.slice(0, k), k);
node.right = createTree(
inorder.slice(k + 1),
postorder.slice(k, postorder.length - 1),
n - k - 1
);
return node;
};
const res = createTree(inorder, postorder, postorder.length);
return res;
};
复杂度
- 时间:n;
- 空间:n;
从前序和后序构造二叉树
题目
- 889;
思路
- 已知前序和后序,无法构造唯一二叉树;
- 度为 1 时,无法确定子树是左右;
- 默认前序第二个值为左子树的根节点;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} preorder
* @param {number[]} postorder
* @return {TreeNode}
*/
var constructFromPrePost = function (preorder, postorder) {
const dfs = (preorder, postorder) => {
const root = preorder[0];
if (root == null) return null;
const leftRoot = preorder[1];
const leftIndex = postorder.indexOf(leftRoot);
const node = new TreeNode(root);
node.left = dfs(
preorder.slice(1, leftIndex + 2),
postorder.slice(0, leftIndex + 1)
);
node.right = dfs(
preorder.slice(leftIndex + 2),
postorder.slice(leftIndex + 1, postorder.length - 1)
);
return node;
};
return dfs(preorder, postorder);
};
复杂度
- 时间:n^2;
- 空间:n^2;
二叉搜索树
基础
二叉搜索树
- 左子树所有节点值 < 根子树节点值 < 右子树所有节点值;
- 二叉搜索树不存在重复节点;
二叉搜索树的操作
查找节点
- 从根节点出发;
- 循环比较节点值;
- 小于节点值:寻找左子树;
- 等于节点值:目标节点;
- 大于节点值:寻找右子树;
function find(value: number): BinarySearchTreeNode | null {
if (this._value === null) return null;
if (this._value === value) return this;
if (this._left && this._value > value) {
return this._left.find(value);
}
if (this._right && this._value < value) {
return this._right.find(value);
}
return null;
}
插入节点
- 查找插入位置:同查找节点;
- 插入节点:若已存在,不插入;
function insert(value: number): boolean {
if (this._value === null) {
this._value = value;
return true;
}
if (this._value > value) {
if (this._left === null) {
this._left = new BinarySearchTreeNode(value);
this._left._parent = this;
return true;
}
this._left.insert(value);
return true;
}
if (this._value < value) {
if (this._right === null) {
this._right = new BinarySearchTreeNode(value);
this._right._parent = this;
return true;
}
this._right.insert(value);
return true;
}
return false;
}
删除节点
- 查找插入位置:同查找节点;
- 删除节点;
- 叶子节点:直接删除;
- 删除节点度为 1;
- 删除节点值替换为子节点;
- 删除原本子节点;
- 删除节点度为 2;
- 寻找右子树最小节点;
- 删除节点值替换为最小节点;
- 删除原本最小节点;
function remove(value: number): boolean {
const node = this.find(value);
if (node === null) return false;
// 2
if (node._left && node._right) {
const minNode = node._right.findMin();
node._value = minNode._value;
if (minNode._right) {
(minNode._parent as BinarySearchTreeNode)._left = minNode._right;
minNode._right._parent = minNode._parent as BinarySearchTreeNode;
minNode._right = null;
}
minNode._parent = null;
return true;
}
// 0
if (!node._left && !node._right) {
if (node._parent) {
if (node._parent._left?._value === value) node._parent._left = null;
if (node._parent._right?._value === value) node._parent._right = null;
}
node._parent = null;
return true;
}
// 1
if (node._left) {
node._value = node._left._value;
node._left._parent = null;
node._left = null;
}
if (node._right) {
node._value = node._right._value;
node._right._parent = null;
node._right = null;
}
return true;
}
二叉搜索树的效率
理想情况
| 时间复杂度 | |
|---|---|
| 查找 | |
| 插入 | |
| 删除 |
退化情况
| 时间复杂度 | |
|---|---|
| 查找 | n |
| 插入 | n |
| 删除 | n |
二叉搜索树题目
验证二叉搜索树
题目
- 98;
思路
- 判断根节点值 root 是否在 [min,max] 内;
- 递归左子树,max 修改为 root;
- 递归右子树,min 修改为 root;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isValidBST = function (root) {
const preorder = (root, min, max) => {
if (root == null) return true;
if (root.val <= min || root.val >= max) return false;
const temp1 = preorder(root.left, min, root.val);
const temp2 = preorder(root.right, root.val, max);
return temp1 && temp2;
};
return preorder(root, -Infinity, Infinity);
};
复杂度
- 时间:n;
- 空间:n;
平衡二叉树
题目
- 110;
思路
- 遍历左右子树,判断其是否平衡;
- 再判断当前树是否平衡;
- 判断机制;
- 计算子树高度判断,平衡返回正常高度,不平衡返回 -1;
- 最后根据子树高度是否为 -1,子树高度差是否为 -1 判断;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isBalanced = function (root) {
const dfs = (node) => {
if (node == null) return 0;
const left = dfs(node.left);
const right = dfs(node.right);
if (left === -1 || right === -1 || Math.abs(left - right) > 1) return -1;
return Math.max(left, right) + 1;
};
return dfs(root) !== -1;
};
复杂度
- 时间:n;
- 空间:n;
删除二叉搜索树中的节点
题目
- 450;
思路
- 查找插入位置:同查找节点;
- 删除节点;
- 叶子节点:直接删除;
- 删除节点度为 1;
- 删除节点值替换为子节点;
- 删除原本子节点;
- 删除节点度为 2;
- 寻找右子树的最左节点;
- 左子树作为最左节点的左子树;
- 返回最左节点;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} key
* @return {TreeNode}
*/
var deleteNode = function (root, key) {
const dfs = (node) => {
if (node == null) return node;
if (node.val > key) node.left = dfs(node.left);
if (node.val < key) node.right = dfs(node.right);
if (node.val === key) {
if (node.left == null && node.right == null) return null;
if (node.left != null && node.right != null) {
let cur = node.right;
while (cur.left != null) {
cur = cur.left;
}
cur.left = node.left;
node.left = null;
return node.right;
}
if (node.left != null) return node.left;
if (node.right != null) return node.right;
}
return node;
};
return dfs(root);
};
复杂度
- 时间:n;
- 空间:1;
寻找二叉搜索树中的目标节点
题目
- 174;
思路
- 根据 "右-根-左" 遍历;
- 第 k 个即第 k 个最大节点;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} cnt
* @return {number}
*/
var findTargetNode = function (root, cnt) {
let node = root;
const stack = [];
while (stack.length !== 0 || node != null) {
while (node) {
stack.push(node);
node = node.right;
}
node = stack.pop();
cnt--;
if (cnt === 0) return node.val;
node = node.left;
}
};
复杂度
- 时间:n;
- 空间:n;
二叉搜索树中第 K 小的元素
题目
- 230;
思路
- 同寻找二叉搜索树中的目标节点,只是换成中序遍历;
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} k
* @return {number}
*/
var kthSmallest = function (root, k) {
let node = root;
const stack = [];
while (node || stack.length !== 0) {
while (node != null) {
stack.push(node);
node = node.left;
}
node = stack.pop();
k--;
if (k == 00) return node.val;
node = node.right;
}
};
复杂度
- 时间:n;
- 空间:n;
将二叉搜索树转换为排序的双向链表
题目
思路
- 基于中序遍历;
- 如果当前节点为空,直接返回;
- 如果不为空;
- 递归左子树;
- 如果尾节点不为空,连接当前节点;
- 如果为空,初始化当前节点为头结点;
- 将当前节点标记为尾节点;
- 遍历右子树;
- 将头节点和尾节点连接;
/**
* // Definition for a Node.
* function Node(val,left,right) {
* this.val = val;
* this.left = left;
* this.right = right;
* };
*/
/**
* @param {Node} root
* @return {Node}
*/
var treeToDoublyList = function (root) {
let head = (tail = null);
const dfs = (node) => {
if (node == null) return;
dfs(node.left);
if (tail != null) {
tail.right = node;
node.left = tail;
} else {
head = node;
}
tail = node;
dfs(node.right);
};
if (root == null) return root;
dfs(root);
head.left = tail;
tail.right = head;
return head;
};
复杂度
- 时间:n;
- 空间:n;
AVL 树
基础
节点高度
- 节点到最远叶节点的距离;
- 叶节点高度为 0;
- 空节点高度为 -1;
get leftHeight ():number {
if (!this._left) return 0
return this._left.height + 1
}
get rightHeight ():number {
if (!this._right) return 0
return this._right.height + 1
}
get height () {
return Math.max(this.leftHeight, this.rightHeight)
}
高度平衡因子
- 左子树高度 - 右子树高度;
- 空节点平衡因子为 0;
- AVL 树中,高度平衡因子范围为 [-1,1]
旋转
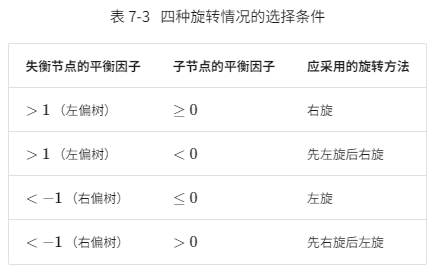
失衡节点
- 高度平衡因子绝对值大于 1 的节点;
function balance(node: AVLTreeNode) {
if (node.leftHeight - node.rightHeight > 1) {
const children = node._left as AVLTreeNode;
if (children.leftHeight > children.rightHeight) {
this.rightRotate(node);
} else {
this.leftRightRotate(node);
}
return true;
} else if (node.leftHeight - node.rightHeight < -1) {
const children = node._right as AVLTreeNode;
if (children.leftHeight > children.rightHeight) {
this.rightLeftRotate(node);
} else {
this.leftRotate(node);
}
return true;
} else {
return false;
}
}
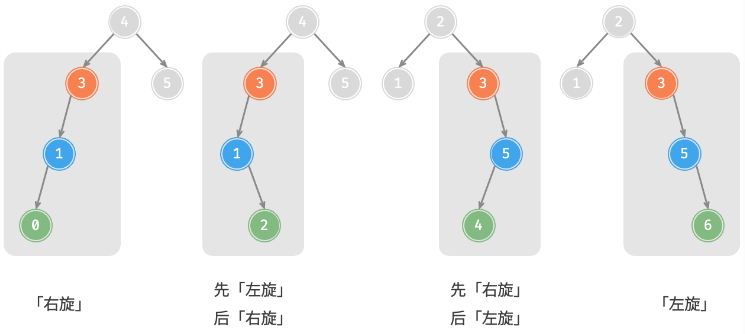
右旋
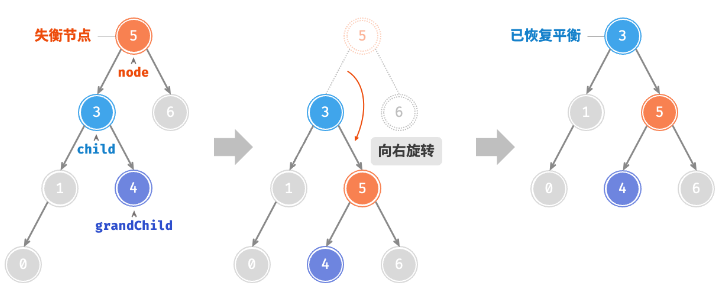
function rightRotate(node: AVLTreeNode) {
const parent = node._parent;
const children = node._left as AVLTreeNode;
node._parent = children;
if (children._right) {
node._left = children._right;
children._right._parent = node;
} else {
node._left = null;
}
children._right = node;
if (parent) {
children._parent = parent;
parent._left = children;
} else {
children._parent = null;
this._root = children;
}
}
左旋
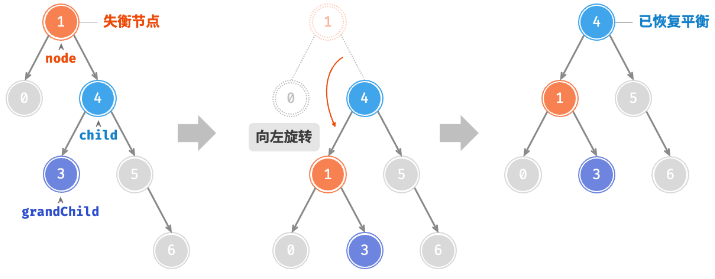
function leftRotate(node: AVLTreeNode) {
const parent = node._parent;
const children = node._right as AVLTreeNode;
node._parent = children;
if (children._left) {
node._right = children._left;
children._left._parent = node;
} else {
node._right = null;
}
children._left = node;
if (parent) {
children._parent = parent;
parent._right = children;
} else {
children._parent = null;
this._root = children;
}
}
先左旋后右旋
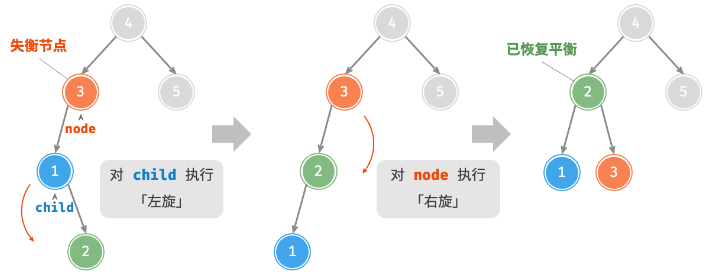
function leftRightRotate(node: AVLTreeNode) {
const children = node._left as AVLTreeNode;
const grandChildren = children._right as AVLTreeNode;
children._parent = grandChildren;
children._right = null;
grandChildren._left = children;
grandChildren._parent = node;
node._left = grandChildren;
this.rightRotate(node);
}
先右旋后左旋
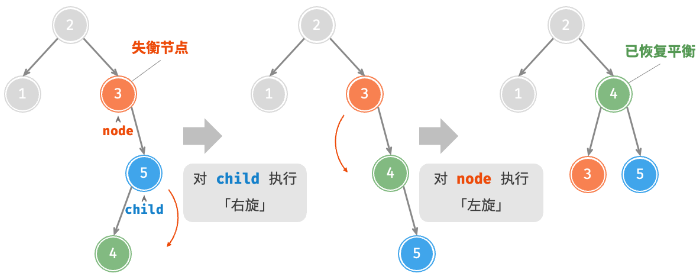
function rightLeftRotate(node: AVLTreeNode) {
const children = node._right as AVLTreeNode;
const grandChildren = children._left as AVLTreeNode;
children._parent = grandChildren;
children._left = null;
grandChildren._right = children;
grandChildren._parent = node;
node._right = grandChildren;
this.leftRotate(node);
}
旋转的选择
AVL 树常用操作
查找节点
- 同二叉搜索树;
插入节点
- 同二叉搜索树插入节点;
- 插入节点后,插入位置从底到顶寻找第一个失衡节点进行旋转;
function insert(value: number) {
this._root.insert(value);
let currentNode = this._root.find(value);
while (currentNode) {
if (this.balance(currentNode)) break;
currentNode = currentNode._parent;
}
}
删除节点
- 同二叉搜索树删除节点;
- 删除节点后对根节点进行旋转;
function remove(value: number) {
this._root.delete(value);
this.balance(this._root);
}
并查集
并查集
- 树形结构;
- 处理集合的合并和查询问题;
操作
- 合并:合并两个集合;
- 查找;
- 查找 x 属于什么集合;
- 查找 x 和 y 是否在同一集合;
实现
快速查询
- 基于数组实现,查询效率高;
- 数组存储集合编号;
- 初始化:数组索引作为每个元素的集合编号;
- 合并:将元素对应的集合编号修改为另外一个集合编号;
- 查找:两个元素集合编号是否一致;
class UnionFind:
def __init__(self, n): # 初始化: 将每个元素的集合编号初始化为数组下标索引
self.ids = [i for i in range(n)]
def find(self, x): # 查找元素所属集合编号内部实现方法
return self.ids[x]
def union(self, x, y): # 合并操作: 将集合 x 和集合 y 合并成一个集合
x_id = self.find(x)
y_id = self.find(y)
if x_id == y_id: # x 和 y 已经同属于一个集合
return False
for i in range(len(self.ids)): # 将两个集合的集合编号改为一致
if self.ids[i] == y_id:
self.ids[i] = x_id
return True
def is_connected(self, x, y): # 查询操作: 判断 x 和 y 是否同属于一个集合
return self.find(x) == self.find(y)
快速合并
- 基于森林 (若干树) 实现,每个树层数为 2;
- 一棵树代表一个集合;
- 树每个节点为元素;
- 根节点为集合的初始元素;
- 使用数组记录森林,fa[x] 保存 x 父节点的节点值;
- 初始化:数组索引作为每个元素的集合编号,即集合初始元素 fa[x] = x;
- 合并:将一个集合的父节点值指向另一个集合编号;
- 查找:不断递归元素的父节点,直至到达根节点,判断根节点是否一致;
class UnionFind {
constructor(n) {
this.fa = new Array(n).map((_, index) => index);
}
find(x) {
while (this.fa[x] !== x) {
this.fa[x] = this.fa[this.fa[x]];
x = this.fa[x];
}
return x;
}
union(x, y) {
indexX = this.fa.indexOf(x);
indexY = this.fa.indexOf(y);
if (indexX !== indexY) {
this.fa[x] = indexY;
}
}
isConnected(x, y) {
return this.find(x) === this.find(y);
}
}
隔代压缩
- 快速合并进行查找操作,效率慢;
- 如果查找过程中,访问的父节点不是根节点;
- 将当前节点的父节点设置为父节点的父节点;
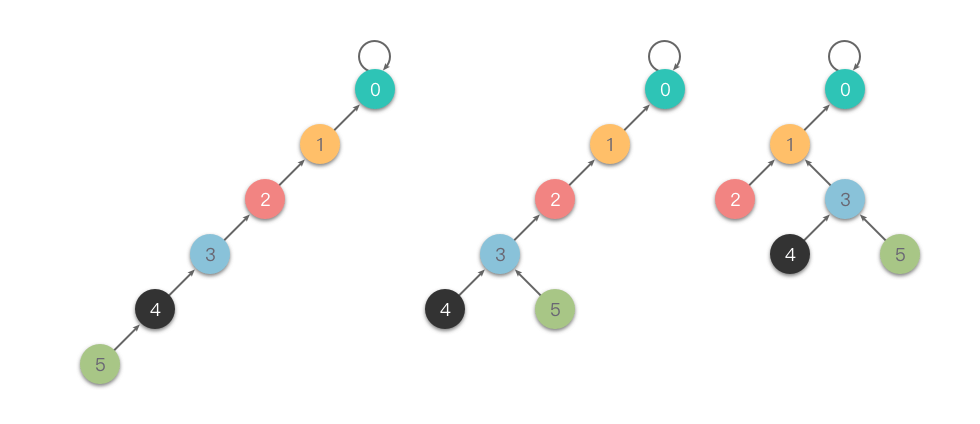
def find(self, x): # 查找元素根节点的集合编号内部实现方法
while self.fa[x] != x: # 递归查找元素的父节点, 直到根节点
self.fa[x] = self.fa[self.fa[x]] # 隔代压缩
x = self.fa[x]
return x # 返回元素根节点的集合编号