字符串
字符串
字符串的比较
- 逐字符比较其字符编码值;
- ASCII;
- Unicode;
存储结构
- 顺序存储结构:数组;
- 链式存储结构:链表;
字符串匹配问题 (模式匹配)
文本串和模式串
- 给定字符串 T 和 P;
- 在 T 中寻找 P;
- T 即文本串,P 即模式串;
单模式匹配问题
概述
- 给定一个文本串和一个特定模式串;
- 寻找模式串的所有出现位置;
方法
- 基于前缀搜索:在搜索窗口中正向搜索,搜索最长公共前缀;
- 基于后缀搜索:在搜索窗口中反向搜索,搜索最长公共后缀;
- 基于子串搜索;
多模式匹配问题
概述
- 给定一个文本串和一组模式串;
- 寻找所有模式串的所有出现位置;
简单方法
- 针对一组模式串种的一个模式串使用单模式匹配算法;
方法
- 基于前缀搜索;
- 基于后缀搜索;
- 基于子串搜索;
字符串基础题目
反转字符串中的单词 1
题目
- 151;
思路
/**
* @param {string} s
* @return {string}
*/
var reverseWords = function (s) {
let cur = "";
let words = [];
for (const ch of s) {
if (ch.match(/\s/)) {
if (cur.length > 0) {
words.push(cur);
cur = "";
}
} else {
cur += ch;
}
}
if (cur.length > 0) words.push(cur);
let left = 0;
let right = words.length - 1;
while (left < right) {
[words[left], words[right]] = [words[right], words[left]];
left++;
right--;
}
return words.join(" ");
};
/**
* @param {string} s
* @return {string}
*/
var reverseWords = function (s) {
return s.trim().split(/\s+/).reverse().join(" ");
};
复杂度
- 时间:n;
- 空间:1;
反转字符串中的单词 3
题目
- 557;
思路
/**
* @param {string} s
* @return {string}
*/
var reverseWords = function (s) {
return s
.split(" ")
.map((word) => word.split("").reverse().join(""))
.join(" ");
};
复杂度
- 时间:n;
- 空间:n;
字符串相乘
题目
- 43;
思路
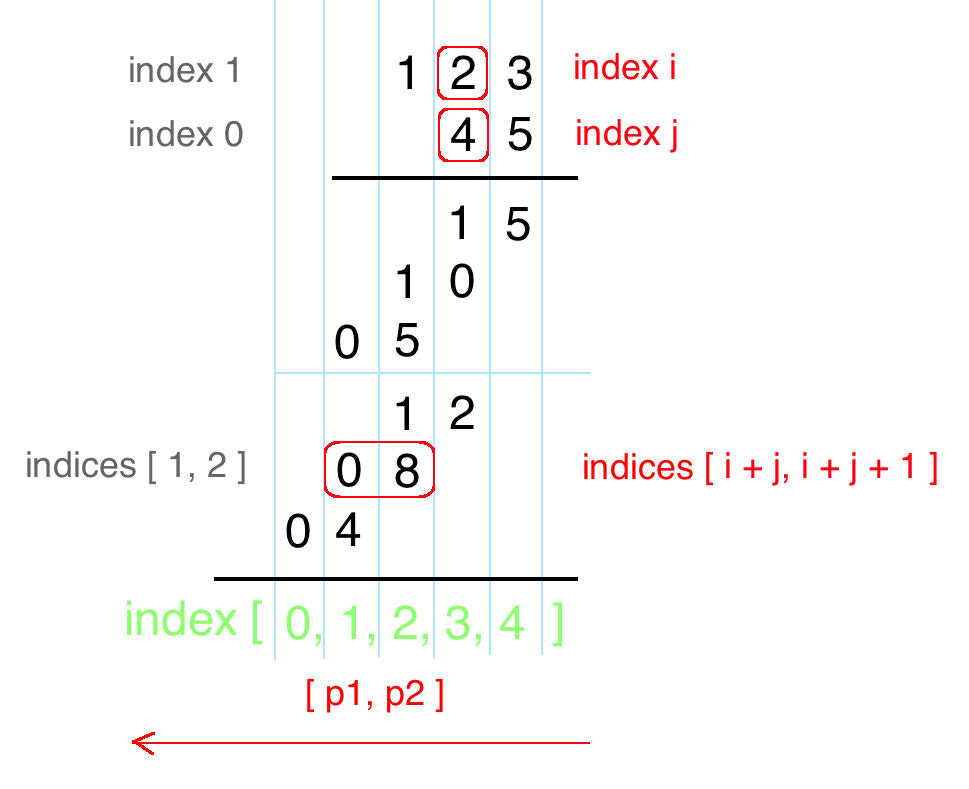
- 若 num1,num2 位数为 M 和 N,最大位数为 M + N;
- nums1[i] * nums2[j] 结果为 "xy",第一位位于 res[i+j],第二位位于 res[i+j+1];
- 最后结果可能存在前导零,需要移除;
/**
* @param {string} num1
* @param {string} num2
* @return {string}
*/
var multiply = function (num1, num2) {
const m = num1.length;
const n = num2.length;
const res = new Array(m + n).fill(0);
for (let i = m - 1; i >= 0; i--) {
for (let j = n - 1; j >= 0; j--) {
const dot = Number(num1[i]) * Number(num2[j]);
let v1 = 0;
let v2 = 0;
if (dot >= 10) {
v1 = Math.floor(dot / 10);
v2 = dot % 10;
} else {
v2 = dot;
}
res[i + j] += v1;
res[i + j + 1] += v2;
}
}
let carry = 0;
for (let i = m + n - 1; i >= 0; i--) {
let value = res[i] + carry;
if (value >= 10) {
carry = Math.floor(value / 10);
value = value % 10;
} else {
carry = 0;
}
res[i] = value;
}
while (res[0] === 0 && res.length > 1) res.shift();
return res.join("");
};
复杂度
- 时间:mn;
- 空间:m+n;
最长公共前缀
题目
- 14;
思路
- 依次遍历所有字符串的每一列,比较相同位置字符是否相同;
- 如果相同,比较下一列;
- 不相同,直接返回当前列之前的部分;
/**
* @param {string[]} strs
* @return {string}
*/
var longestCommonPrefix = function (strs) {
for (let i = 0; i < strs[0].length; i++) {
const ch = strs[0][i];
for (let j = 1; j < strs.length; j++) {
if (strs[j][i] !== ch) {
return strs[0].slice(0, i);
}
}
}
return strs[0];
};
复杂度
- 时间:m * n;
- 空间:1;
字符串转换整数
题目
- 8;
思路
- 移除空格;
- 判断是否存在符号位;
- 判断是否为有效数字,使用字符串存储;
- 字符串转换整数;
- 截断至 32 为有符号整数范围;
/**
* @param {string} s
* @return {number}
*/
var myAtoi = function (s) {
s = s.trim();
let sign = 1;
let start = 1;
let numStr = "";
if (s[0] === "+") sign = true;
else if (s[0] === "-") sign = false;
else start = 0;
for (let i = start; i < s.length; i++) {
const ch = s[i];
if (!ch.match(/\d/)) break;
numStr += ch;
}
const num = Number(numStr);
if (sign) {
return Math.min(num, 2 ** 31 - 1);
} else {
return Math.max(-num, -(2 ** 31));
}
};
复杂度
- 时间:n;
- 空间:1;
验证 IP 地址
题目
- 468;
思路
- 判断 IPV4;
- 根据 。分割数组;
- 逐元素判断;
- 元素长度小于 3,大于 1;
- 不能存在前导零,0 只能是单个字符;
- 数值在 0 - 255;
- 判断 IPV6;
- 根据 :分割数组;
- 逐元素判断;
- 元素长度小于 4,大于 1;
- 允许前导零;
- 判断元素诸位是否为有效字符;
/**
* @param {string} queryIP
* @return {string}
*/
var validIPAddress = function (queryIP) {
let arr = queryIP.split(".");
if (arr.length === 4) {
for (let i = 0; i < 4; i++) {
const sub = arr[i];
if (!/^\d+$/.test(sub)) return "Neither";
const num = Number(sub);
if (num < 0 || num > 255) return "Neither";
if (sub[0] === "0" && sub.length != 1) return "Neither";
}
return "IPv4";
}
arr = queryIP.split(":");
if (arr.length === 8) {
for (let i = 0; i < 8; i++) {
const sub = arr[i];
if (!/^[a-fA-F0-9]{1,4}$/.test(sub)) return "Neither";
}
return "IPv6";
}
return "Neither";
};
复杂度
- 时间:n;
- 空间:n;
最长回文串
题目
- 409;
思路
- 回文字符串有偶数数量的字符串 + 可能存在的数量为 1 字符串;
- 使用 hash 记录各字符频数;
- 通过对频数对 2 取余,取偶数数量的频数,even+=偶数数量频数;
- 判断剩余频数是否为 1,对 odd 进行赋值;
/**
* @param {string} s
* @return {number}
*/
var longestPalindrome = function (s) {
const hash = {};
for (const ch of s) {
if (hash[ch] == null) hash[ch] = 1;
else hash[ch]++;
}
let even = 0;
let odd = 0;
for (let value of Object.values(hash)) {
const temp = value % 2;
even += value - temp;
if (temp === 1) odd = 1;
}
return even + odd;
};
复杂度
- 时间:n;
- 空间:n;
字符串双指针题目
比较版本号
题目
- 165;
思路
- 根据 。分割字符串;
- 数组字符串转换为数字,缺失值赋值为 0;
- 逐元素比较数组大小;
/**
* @param {string} version1
* @param {string} version2
* @return {number}
*/
var compareVersion = function (version1, version2) {
const arr1 = version1.split(".").map((value) => Number(value));
const arr2 = version2.split(".").map((value) => Number(value));
const len = Math.max(arr1.length, arr2.length);
for (let i = 0; i < len; i++) {
const value1 = arr1[i] || 0;
const value2 = arr2[i] || 0;
if (value1 > value2) return 1;
else if (value1 < value2) return -1;
else continue;
}
return 0;
};
复杂度
- 时间:n;
- 空间:n;
反转字符串
题目
- 344;
思路
- 双指针即可;
/**
* @param {character[]} s
* @return {void} Do not return anything, modify s in-place instead.
*/
var reverseString = function (s) {
const n = s.length;
let left = 0;
let right = n - 1;
while (left < right) {
[s[left], s[right]] = [s[right], s[left]];
left++;
right--;
}
return s;
};
复杂度
- 时间:n;
- 空间:n;
单模式串匹配
Brute Force 算法
简述
- 暴力匹配算法;
- 给定文本串 T 和模式串 P;
- 从 T 第一个字符开始和 P 第一个字符比较;
- 如果相等,继续比较下一字符;
- 若不相等,从 T 第二个字符重新比较;
- 依次类推;
算法步骤
def bruteForce(T: str, p: str) -> int:
n, m = len(T), len(p)
i, j, start = 0, 0, 0 # i 表示文本串 T 的当前位置, j 表示模式串 p 的当前位置
while i < n and j < m: # i 或 j 其中一个到达尾部时停止搜索
if T[i] == p[j]: # 如果相等, 则继续进行下一个字符匹配
i += 1
j += 1
else:
i = start + 1 # 如果匹配失败则将 i 移动到上次匹配开始位置的下一个位置
start += 1
j = 0 # 匹配失败 j 回退到模式串开始位置
if j == m:
return i - j # 匹配成功, 返回匹配的开始位置
else:
return -1 # 匹配失败, 返回 -1
时间复杂度
- 平均:m+n;
- 最坏:m * n;
KMP 算法
优化思想
- 对于文本串和模式串;
- 当文本串和模式串不匹配时,利用匹配失败的信息;
- 尽量减少模式串和文本串的匹配次数;
前缀表
- 使用 next 数组;
- next[i] 表示模式串 [0,i] 中,前 k 个字符等于后 k 个字符中,最大的 k;
比较原理
- 如果文本串 T 与模式串 P 的匹配失败实在 T[i] 与 P[j] 比较发生;
- 说明 T[i-j:i]==P[0:j],即两者前 j 个字符相等;
- 前 j 个字符对应 next[j-1],设为 k;
- 文本串子串的后 k 位和匹配串前 k 位相等,即 T[i-k:i] = P[0:k];
- 所以从 T[i] 和 P[k] 比较即可;
- 具体代码见字符串匹配题目 - 找出字符串中第一个匹配项的下标;
单模式串匹配题目
找出字符串中第一个匹配项的下标
题目
- 28;
思路
- 单模式串匹配;
/**
* @param {string} haystack
* @param {string} needle
* @return {number}
*/
var strStr = function (haystack, needle) {
const generateNext = (p) => {
const next = new Array(p.length).fill(0);
let left = 0;
for (let right = 1; right < p.length; right++) {
while (left > 0 && p[left] !== p[right]) {
left = next[left - 1];
}
if (p[left] === p[right]) {
left++;
}
next[right] = left;
}
return next;
};
const kmp = (T, p) => {
const next = generateNext(p);
let j = 0;
for (let i = 0; i < T.length; i++) {
while (j > 0 && T[i] !== p[j]) {
j = next[j - 1];
}
if (T[i] === p[j]) {
j++;
}
if (j === p.length) {
return i - j + 1;
}
}
return -1;
};
const res = kmp(haystack, needle);
return res;
};
复杂度
- 时间:m + n;
- 空间:n;
重复的子字符串
题目
- 459;
思路
- 基于 kmp 算法;
- next[i] 即 p[0:i] 中最长前后缀的长度;
- 如果该字符串可以通过重复子字符串 a 组成,s = a*n;
- 当 i = s.length 时,next[i] 大于 0 且为 a*(n-1);
- 即
s.length % (s.length - next.at(-1)) === 0);
/**
* @param {string} s
* @return {boolean}
*/
var repeatedSubstringPattern = function (s) {
const generate = (p) => {
const next = new Array(p.length).fill(0);
let left = 0;
for (let right = 1; right < p.length; right++) {
while (left > 0 && p[left] !== p[right]) {
left = next[left - 1];
}
if (p[left] === p[right]) left++;
next[right] = left;
}
return next;
};
const next = generate(s);
if (next.at(-1) > 0 && s.length % (s.length - next.at(-1)) === 0) return true;
return false;
};
复杂度
- 时间:n;
- 空间:n;
字典树
基础
- 又称前缀树;
- 单词在字典树中表现为从根节点触发的路径;
基本性质
- 根节点不包含字符,其余节点只包含一个字符;
- 从根节点到某个节点的路径,即某个节点对应的字符串;
- 节点的子节点的字符不同;
字典树结构
节点结构
class Node: # 字符节点
def __init__(self): # 初始化字符节点
self.children = dict() # 初始化子节点
self.isEnd = False # isEnd 用于标记单词结束
插入
- 遍历单词 ch,从根节点的子节点位置进行插入操作;
- 如果不存在对应子节点,创建一个子节点,然后指向新建立的子节点,处理下一个字符;
- 反之直接指向对应子节点,处理下一个字符;
- 单词处理完毕,将当前节点标记为单词结束;
创建
- 初始化字典树;
- 遍历所有单词,一一插入即可;
查找单词
- 遍历单词 ch,从根节点的子节点位置进行查找操作;
- 如果不存在对应子节点,返回 false;
- 反之指向对应子节点,处理下一个字符;
- 单词处理完毕时,判断当前节点是否有单词结束标识,有则返回 true,反之 false;
查找前缀
- 在查找单词的基础上,不需要判断单词结束标识;
字典树题目
实现 Trie (前缀树)
题目
- 208;
思路
function TreeNode(val) {
this.val = val;
this.children = new Map();
this.isEnd = false;
}
var Trie = function () {
this.root = new TreeNode();
};
/**
* @param {string} word
* @return {void}
*/
Trie.prototype.insert = function (word) {
let cur = this.root;
for (const ch of word) {
if (cur.children.has(ch)) cur = cur.children.get(ch);
else {
cur.children.set(ch, new TreeNode(ch));
cur = cur.children.get(ch);
}
}
cur.isEnd = true;
};
/**
* @param {string} word
* @return {boolean}
*/
Trie.prototype.search = function (word) {
let cur = this.root;
for (const ch of word) {
if (cur.children.has(ch)) cur = cur.children.get(ch);
else return false;
}
return cur.isEnd;
};
/**
* @param {string} prefix
* @return {boolean}
*/
Trie.prototype.startsWith = function (prefix) {
let cur = this.root;
for (const ch of prefix) {
if (cur.children.has(ch)) cur = cur.children.get(ch);
else return false;
}
return true;
};
/**
* Your Trie object will be instantiated and called as such:
* var obj = new Trie()
* obj.insert(word)
* var param_2 = obj.search(word)
* var param_3 = obj.startsWith(prefix)
*/
字典序的第 k 小数字
题目
- 440;
思路
- 基于字典序和前序遍历;
- 直接建立和遍历的话超时;
- 不用要使用前序遍历,而是通过数学方法求出移动至另一个节点需要走几步;
- 这个公式建议死记硬背吧;
- 如果步数大于 k,说明第 k 个元素在当前节点内,反之在另一个节点;
/**
* @param {number} n
* @param {number} k
* @return {number}
*/
var findKthNumber = function (n, k) {
const getStep = (n, cur, next) => {
let step = 0;
while (cur <= n) {
step += Math.min(next, n + 1) - cur;
cur *= 10;
next *= 10;
}
return step;
};
let step = 1;
let res = 1;
while (step < k) {
const temp = getStep(n, res, res + 1);
if (step + temp > k) {
step++;
res *= 10;
} else {
step += temp;
res++;
}
}
return res;
};
复杂度
- 时间:n;
- 空间:1;