跳到主要内容

关系数据模型

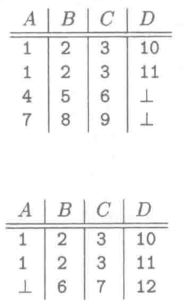
关系模式​

基本术语​

  • 关系：二维表；
  • 列：关系的列；
  • 模式：关系名极其属性的集合；
  • 元组：关系中处属性行之外的其他行；
  • 分量：元组中的对应属性值；
  • 域：分量的类型；
  • 实例：给定关系中元组的集合；
  • 键：定义在键上的属性值唯一；

SQL 中的关系​

  • 表：存储的关系，用于能对其元组进行查询和更新；
  • 视图：通过计算定义的关系；
  • 临时表：执行 SQL 是临时构造；

数据类型​

  • 可变长度/固定长度字符串；
  • 可变长度/固定长度位串；
  • 布尔值；
  • 整数类型；
  • 浮点类型；
  • 日期；
  • 时间；

键的声明​

  • 键的属性值唯一；
    • PRIMARY KEY：属性值不能为 NULL；
    • UNIQUE：属性值可以为 NULL；

代数查询语言​

关系代数概述​

  • 关系操作：交/并/差；
  • 去除行/列的操作：选择/投影；
  • 组合元组的操作：笛卡尔积/连接；
  • 重命名操作；

集合操作​

  • 设两个关系 R 和 S；
  • 并：结果元素来自 R 或 S；
  • 交：结果元素 R 和 S 都存在；
  • 差：R - S 为 R 中存在但 S 中不存在；

投影​

  • π\pi
  • 从关系 R 生成新关系 S；
  • S 只包含 R 的部分列；

选择​

  • σC\sigma_C；
  • 从关系 R 中生成一个 R 的元组的子集；

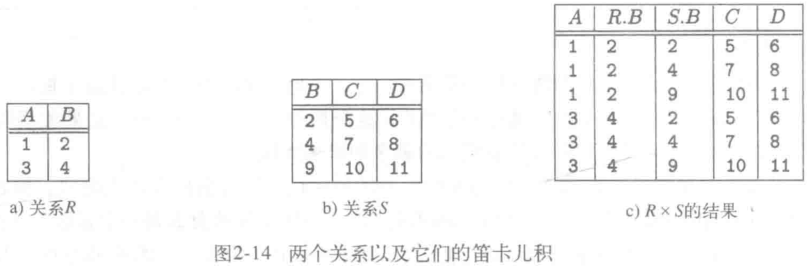
笛卡尔积​

  • 设两个关系 R 和 S；
  • R 和 S 的笛卡尔积 (R×SR \times S) 是一个有序对的集合；
    • 有序对的前半部分是 R 中的任一元组；
    • 有序对的后半部分是 S 中的任一元组；

笛卡尔积

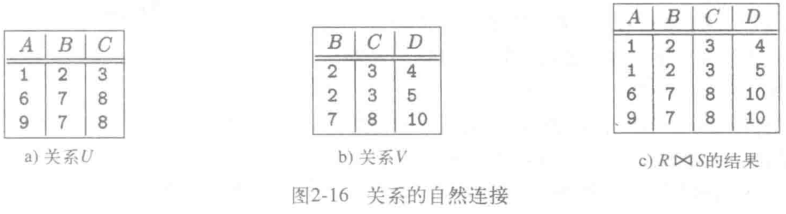
自然连接​

  • 设两个关系 R 和 S；
  • R 和 S 的自然连接 (R⋈SR \Join S) 将 R 和 S 的所有共有属性且属性值相同的元组配对；

自然连接

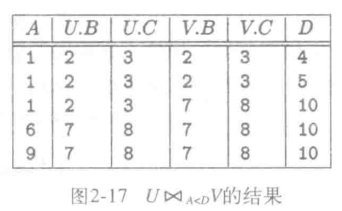
θ\theta 连接​

  • 设两个关系 R 和 S；
  • R 和 S 满足条件 C 的 θ\theta 连接 (R⋈CSR \Join_C S)；
    • 首先得到 R 和 S 的笛卡尔积；
    • 从笛卡尔积寻找满足条件 C 的元组；

连接

命名和重命名​

  • 修改属性名；

操作之间的联系​

  • 一些关系代数操作可以使用其他关系代数操作表示；
  • 六个操作无法被其他操作表示；
    • 并/差/选择/投影/笛卡尔积/重命名；

R∩S=R−(R−S)R \cap S = R-(R-S) R⋈CS=σC(R×S)R \Join_C S = \sigma_C(R\times S) R⋈S=πL(σC(R×S))R \Join S = \pi_L(\sigma_C(R\times S))

关系上的约束​

引用完整性约束​
  • 规定某个关系出现的所有元组必须在另外一个关系出现；
键约束​
  • 关系任意元组键上的属性值不同；
其他约束​
  • 域约束；
    • 属性值的类型约束；
    • 属性值的长度约束；
    • 属性值的取值约束；
  • 。。。；

包​

包​

  • 同一个元组可以多次出现；

包的操作​

  • 包的操作将元组视为独立个体；
  • 操作结果不必去除重复元组；
  • 可以出现多个重复的元组；

包的拓展操作​

消重复操作符​
  • 去重包中的重复元组；
聚集操作符​
  • 聚集操作符：作用于包的列，进行求和/平均等操作；
分组操作符​
  • 根据若干列属性上的属性值将元组分组；
拓展投影​
  • 投影的拓展；
  • 以列为单元进行计算，可以产生新的列；
排序算子​
  • 根据若干属性进行排序；

外连接​

悬浮元组​
  • 连接中无法匹配的元组；
外连接符​
  • 在连接的基础上；
  • 悬浮元组使用 null 补齐；

外连接符

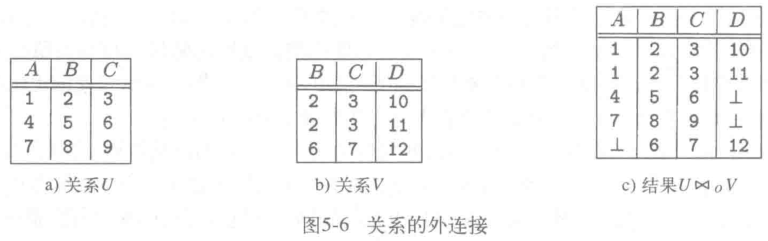
左外连接和右外连接​
  • 左外连接：只对左表进行 null 补齐；
  • 右外连接：只对右表进行 null 补齐；

左外连接和右外连接