二维极坐标空间
使用二维极坐标定位点
定位点
r 的取值范围
- [−∞,∞];
- 当 r < 0 时被认为向后移动;
角度的取值范围
- [−∞,∞];
规范坐标

转换方法

笛卡尔坐标和极坐标的转换
笛卡尔坐标和极坐标的转换
x=rcosθy=rsinθ
r=x2+y2
θ=arctan(xy)

三维极坐标空间
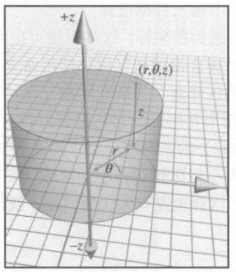
圆柱坐标
圆柱坐标
- (r,θ,z);
球面坐标
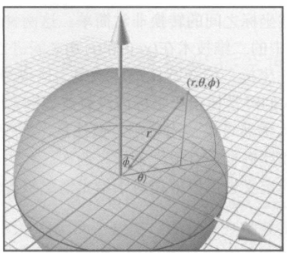
球面坐标
- 右手坐标系;
- (r,θ,ϕ);
- 依次为距离,方位角,天顶角;
方位角
- 起始方向对应于 +x;
- +y 的右手坐标系为正方向;
天顶角
- 起始方向对应于 +z;
- +x 的右手坐标系为正方向;
图形学中球面坐标的转换
图形学中球面坐标的转换
- 水平角度重命名为 h;
- 起始方向对应于 +z;
- +y 的左手坐标系为正方向;
- 垂直角度重命名为 p;
- 起始方向对应于 +x;
- +x 的左手坐标系为正方向;

球面坐标的别名
规范坐标

转换方法

笛卡尔坐标和极坐标的转换
右手坐标系
x=rsinϕcosθy=rsinϕsinθz=rcosϕ
左手坐标系
x=rcospsinhy=−rsinpz=rcospcosh
r=x2+y2+z2
h=atan2(x,z)
p=arcsin(r−y)
使用极坐标指定向量
使用极坐标指定向量







