坐标空间

为什么需要多个坐标空间

原因

• 某些信息仅在特定坐标系中是已知的；
• 例如一个点 a，我们可能不知道其在世界坐标系中的位置；
• 但我们或许表达 a 相对于其他坐标系的位置；

有用的坐标空间

世界空间(全局坐标空间/通用坐标空间)

• 坐标：球面坐标；
• 原点：[0，0]；

对象空间(体空间)

• 与特定对象关联的坐标空间；
• 每个对象都有自己独立的对象空间；

相机空间

• 与用于渲染的视点相关联的对象空间；
• 使用左手坐标系；
• 原点为相机；

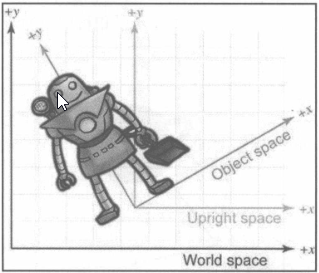
直立空间

• 世界空间和对象空间转换的中间坐标空间；
• 直立空间轴线与世界空间平行；
• 直立空间原点和对象空间原点重合；

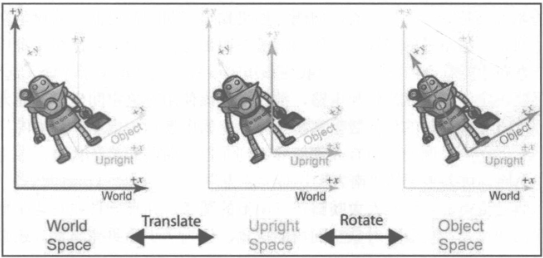
直立空间的转换

• 对象空间 - 直立空间：旋转；
• 直立空间 - 世界空间：平移；

基向量和坐标空间转换

基向量

• p，q，r 是三维空间的基向量；
• v 为基向量的线性组合；
• 世界空间的基向量一般为 [1，0，0]，[0，1，0]，[0，0，1]

$v=xp+yq+zr$

良好的基向量

• 一般选择相互垂直的基向量；
• Span(p，q，r) 线性无关；

正交基

• 相互垂直的基向量；

标准正交基

• 单位长度的正交基；

转换公式

• 已知对象空间在直立空间表示的标准正交基为 p，q，r；
• u 为直立空间中的坐标；
• b 为对象空间的坐标；

$u_x = bp \qquad u_y= bq \qquad u_z = br$