向量

基础

向量下标表示法

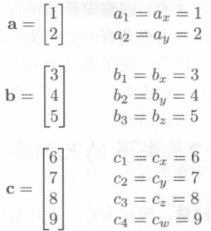
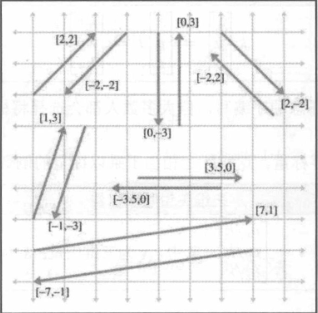
向量的几何意义

大小和方向

• 大小：向量的长度；
• 方向：向量在空间中的方向；

向量的头部和尾部

• 头部：向量的终点；
• 尾部：向量的起点；

使用笛卡尔坐标指定向量

二维向量

• [x，y]；

三维向量

• [x，y，z]；

向量分解

• 向量可以分解为按轴向对齐的分量，分量大小即 x，y，z；

零向量

• 没有大小和方向；

• $[0,\cdots,0]$

向量与点

向量和点的关系

• 向量可以描述相对位置；
• 向量描述了原点到点的位移；
• 任何点都可以表示为来自原点的向量；

负向量

线性代数规则

几何意义

几何意义

• 产生大小相同但方向相反的向量；

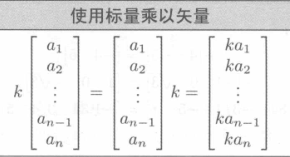
标量和矢量的乘法

线性代数规则

线性代数规则

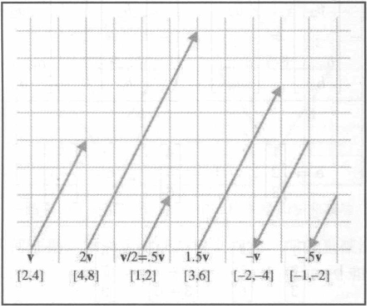
几何解释

几何解释

• 方向不变，大小缩放 k 倍；

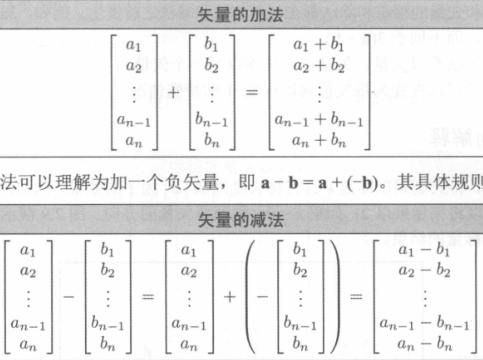
向量的加减法

线性代数规则

线性代数规则

交换

• 向量加法可以交换；
• 向量减法是反交换；

$a+b=b+a$ $a-b=-(b-a)$

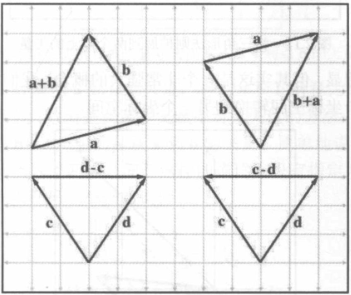
几何解释

三角形法则

• 向量 a 和 b 相加；
• 使 a 的头部与 b 的尾部向量；
• 绘制从 a 的尾部到 b 的头部的向量；
• 适用于向量的加减法；
• 可拓展至 n 个向量的加减法；

从一点到另一点的位移向量

计算方法

• 点 a 到点 b；
• 位移向量为 b - a；

向量大小

线性代数规则

线性代数规则

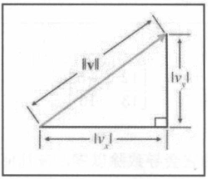
几何解释

几何解释

• 直角三角形的斜边；

单位向量

单位向量和法线

单位向量和法线

• 单位向量强调大小为 1；
• 法线强调法线向量与某物垂直，大小通常为 1；

线性代数规则

线性代数规则

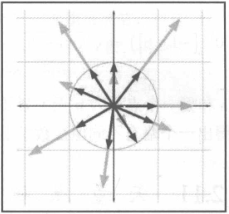
几何解释

几何解释

• 尾部为原点；
• 头部为向量方向与原点为中心的单位圆(球)的交点；

距离公式

距离公式

向量点积 (内积)

线性代数规则

向量点积

• 结果为标量；

$a \cdot b = \sum^n_{i=1}a_ib_i$ $a \cdot b = a_xb_x + a_yb_y$ $a \cdot b = a_xb_x + a_yb_y + a_zb_z$

交换律

• 向量点积是可交换的；

$a \cdot b = b \cdot a$

结合律

点积的加减法分布

$a \cdot (b+c) = a \cdot b + a \cdot c$

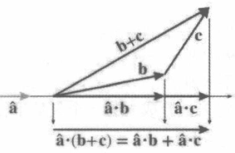
几何解释

投影

• $a \cdot b$ 解释为 b 投影到 a 的任意平行线上的有符号长度，乘以 a 的长度；

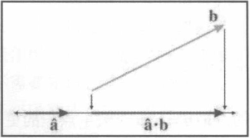
特定方向上的位移

• a 为单位向量，b 为任意长度的向量；
• $a \cdot b$ 解释为 b 在 a 方向上的位移；

向量分解

• a 为单位向量，b 为任意长度的向量；

$b_{\parallel}=(a \cdot b)a$ $b_{\perp}=b-(a \cdot b)a$

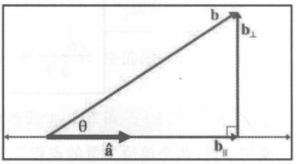
三角函数解释

• a 和 b 的点积是 a 到 b 的角度的余弦；

$a \cdot b = |a||b|cos\theta$

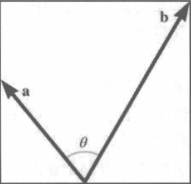
向量叉积

线性代数规则

线性代数规则

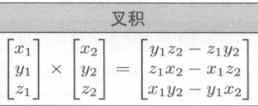
交换律

$a \times b = -(b \times a)$

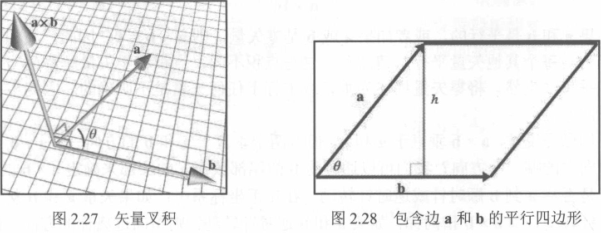
几何解释

大小

• a 和 b 的叉乘的长度等于 a 和 b 大小的乘积再乘以 a 到 b 的角度的正弦值；
• a 和 b 的叉乘的长度 a 和 b 构成的平行多边形的面积；

$|a \times b| = |a||b|\sin\theta$

方向

• 根据坐标系选择旋转法则；
• 拇指指向 a，食指指向 b，方向即中指方向；

基本轴的叉积

线性代数恒等式

线性代数恒等式