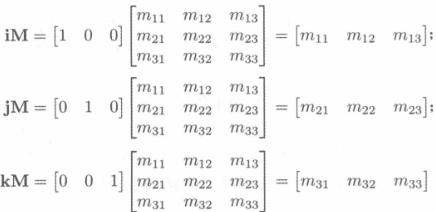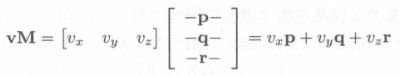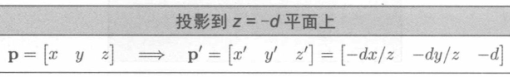矩阵

矩阵的数学定义

矩阵维度和表示法

矩阵维度

• 具有 r 行 c 列的矩阵；
• 称作 $r \times c$；

表示法

• 下标表示法；

$$\begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix}$$

方形矩阵

方形矩阵

• 具有相同行数和列数的矩阵；

对角元素

• 行和列索引相同的元素；

对角矩阵

• 非对角元素均为 0；

$$\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 3 \end{bmatrix}$$

单位矩阵

• 对角元素为 1，其余元素为 0，称作 I；

$$\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

作为矩阵的向量

行向量和列向量

• 行向量：$1 \times n$；
• 列向量：$n \times 1$；

矩阵转置

矩阵转置

• $r \times c$ 矩阵 M；
• 其转置矩阵 $c \times r, \quad M^T$ 即 M 行列翻转；

性质

• $(M^T)^T=M$；
• 对角矩阵 D，$D^T=D$；

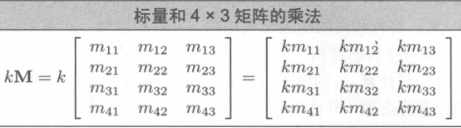
矩阵和标量相乘

矩阵和标量相乘

矩阵相乘

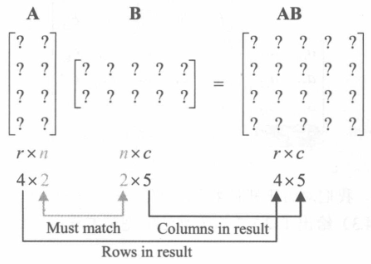
矩阵相乘

• $r \times n$ 矩阵 A 可与 $n \times c$ 矩阵 B 相乘；
• 结果为 $r \times c$ 矩阵 C；

计算公式

• 对于 C 中的第 i 行，第 j 列的元素；
• 对应 A 中的第 i 行，B 中的第 j 列；
• A 和 B 的行和列的对应元素相乘求和；

$c_{ij} = \sum^n_{k=1}a_{ik}b_{kj}$

性质

• MI = IM = M；
• $AB \neq BA$；
• (AB)C = A(BC)；
• (kA)B = k(AB) = A(kB)；
• $(AB)^T = B^TA^T$

向量和矩阵相乘

向量和矩阵相乘

• 行向量位于左侧，结果为行向量；
• 列向量位于右侧，结果为列向量；

矩阵的几何解释

矩阵的几何解释

• 矩阵表示空间坐标变换；
• 矩阵的行可解释为坐标空间的基向量；
• 向量乘矩阵从一个坐标空间变换为另一个坐标空间；
  • 对于标准基向量，标准基向量乘矩阵即经过矩阵变换后的坐标空间的基向量；
• p，q，r 表示一组基向量；

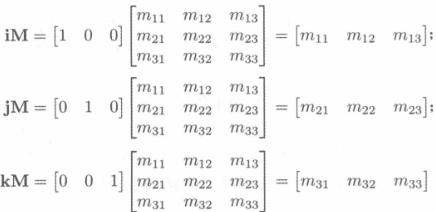
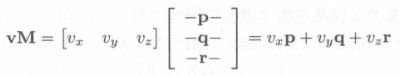
矩阵变换

旋转

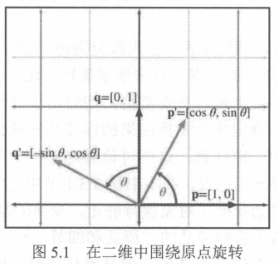
二维旋转矩阵

$$\begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}$$

围绕 x 轴的三维旋转

$$\begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\theta & sin\theta \\ 0 & -sin\theta & cos\theta \end{bmatrix}$$

围绕 y 轴的三维旋转

$$\begin{bmatrix} cos\theta & 0 & sin\theta \\ 0 & 1 & 0 \\ sin\theta & 0 & cos\theta \end{bmatrix}$$

围绕 z 轴的三维旋转

$$\begin{bmatrix} cos\theta & sin\theta & 0 \\ -sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

围绕任意轴的三维旋转

• 看看就行；

缩放

k 因子

• k < 1：缩小；
• k = 1：不变；
• k > 1：拉伸；
• k = 0：正交投影；

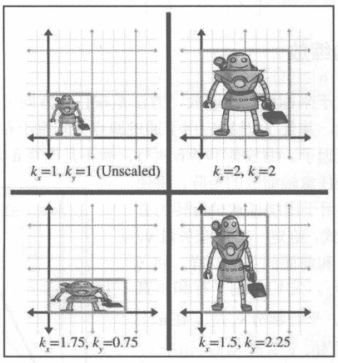
沿主轴缩放的二维矩阵

$$\begin{bmatrix} k_x & 0 \\ 0 & k_y \end{bmatrix}$$

沿主轴缩放的三维矩阵

$$\begin{bmatrix} k_x & 0 & 0 \\ 0 & k_y & 0 \\ 0 & 0 & k_z \end{bmatrix}$$

任意方向缩放的二维矩阵

任意方向缩放的三维矩阵

正交投影

投影到 x 轴

$$\begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}$$

投影到 y 轴

$$\begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix}$$

投影到 xy 平面

$$\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}$$

投影到 yz 平面

$$\begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

投影到 zx 平面

$$\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

投影到任意线的二维矩阵

投影到任意平面的三维矩阵

反射

反射和缩放

• 当缩放矩阵的 k 值 为 -1 时；
• 即对对应轴进行反射；

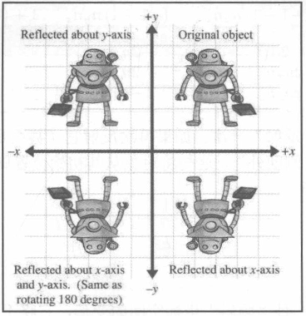
任意轴反射的二维矩阵

任意平面反射的三维矩阵

错切

x 的二维错切矩阵

• x' = x + sy；

$$\begin{bmatrix} 1 & 0 \\ s & 1 \end{bmatrix}$$

y 的二维错切矩阵

• y' = sx + y；

$$\begin{bmatrix} 1 & s \\ 0 & 1 \end{bmatrix}$$

三维错切矩阵

$$H_{xy} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ s & t & 1 \end{bmatrix}$$ $$H_{yz} = \begin{bmatrix} 1 & s & t \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ $$H_{zx} = \begin{bmatrix} 1 & 0 & 0 \\ s & 1 & t \\ 0 & 0 & 1 \end{bmatrix}$$

组合变换

组合变换

• 多个矩阵变换的乘积；

变换的分类

线性函数

• 当下列公式成立时，映射 F 为线性的；

$F(a+b) = F(a) + F(b)$ $F(ka) = kF(a)$

线性变换

• 通过矩阵乘法实现的变换都是线性变换；

$F(a+b) = (a + b)M = aM + bM = F(a) + F(b)$ $F(ka) = (ka)M = k(aM) = kF(a)$

仿射变换

• 符合下列形式的变换都是仿射变换；
  • 本章所有变换 + 平移；

$v' = vM + b$

可逆变换

• 符合下列形式的变换都是可逆变换；

$F^{-1}(F(a)) = F(F^{-1}(a)) = a$

保持角度的变换

• 变换后角度的大小和方向没有变换；
  • 平移 + 旋转 + 均匀缩放；

正交变换

• 保留长度，角度，面积和体积的大小的变换；
  • 平移 + 旋转 + 反射；
• 所有的正交变换都是仿射和可逆的；

刚体变换

• 不改变其形状的变换；
  • 平移 + 旋转；
• 所有的刚体变换都是正交的，保持角度的；

矩阵的行列式

二维矩阵和三维矩阵的行列式

二维矩阵的行列式

$$|M| = \begin{bmatrix} 1 & s \\ 0 & 1 \end{bmatrix}= m_{11}m_{22}-m_{12}m_{21}$$

三维矩阵的行列式

三维矩阵行列式与三维矢量三重积

子矩阵行列式和余子式

子矩阵行列式

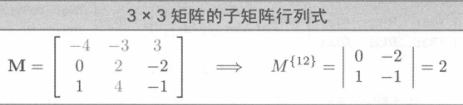
矩阵的余子式

$C^{ij} = (-1)^{i+j}M^{ij}$

任意维度矩阵的行列式

任意维度矩阵的行列式

$|M|=\sum^n_{j=1}m_{ij}C^{ij}=\sum^n_{j=1}m_{ij}(-1)^{i+j}M^{ij}$

行列式的重要特性

单位矩阵的行列式

$|I|=1$

矩阵乘积的行列式

$|AB|=|A||B|$

转置矩阵的行列式

$|M^T|=|M|$

行或列全为 0 的矩阵

• 若矩阵某行或某列全为零；
• 该矩阵行列式为 0；

交换行或列

• 若矩阵交换某行或某列；
• 该矩阵行列式变负；

某行添加到另一行

行列式的几何解释

二维矩阵

• 基向量构成的平行四边形的面积；

三维矩阵

• 基向量构成的平行六面体的体积；

逆矩阵

基础

$M(M^{-1})=M^{-1}M=I$

经典伴随矩阵

经典伴随矩阵

• 计算矩阵的逆矩阵；

逆矩阵

计算公式

$M^{-1} = \frac{adjM}{|M|}$

重要特性

• 矩阵的逆矩阵的逆矩阵是原始矩阵；
• 单位矩阵的逆矩阵是自己；
• 矩阵转置的逆矩阵是逆矩阵的转置；
• 矩阵乘积的逆等于矩阵的逆的乘积；
• 逆矩阵的行列式是原始矩阵行列式的倒数；

$(M^{-1})^{-1}=M$ $I^{-1}=I$ $(M^T)^{-1}=(M^{-1})^T$ $(AB)^{-1}=B^{-1}A^{-1}$ $|M^{-1}|=\frac{1}{|M|}$

逆矩阵的几何解释

逆矩阵的几何解释

• 撤销原始矩阵变换；

正交矩阵

正交矩阵

正交矩阵

• 正交矩阵满足以下公式；

$MM^T=I$ $M^T = M^{-1}$

正交矩阵的几何解释

正交矩阵的解释

• 矩阵每行为单位向量；
• 矩阵的行相互垂直；
• 即标准正交基；

矩阵的正交化

Gram-Schmidt 正交化

4*4 齐次矩阵

四维齐次空间

二维齐次坐标

• (x，y，w)；
• (x，y) 用齐次坐标表示为 (x，y，1)；
• (x，y，w) 映射到 (x/w，y/w)；

三维齐次坐标

• (x，y，z，w)；
• (x，y，z) 用齐次坐标表示为 (x，y，z，1)；
• (x，y，z，w) 映射到 (x/w，y/w，z/w)；
• 当 w = 0 时称为无限远的点；

平移矩阵

三维变换矩阵拓展至四维

平移矩阵

一般仿射变换

一般仿射变换

• 首先经过平移矩阵平移到原点；
• 在原点执行三维变换矩阵；
• 通过平移矩阵的逆矩阵返回值原来位置；

$TR(T^{-1})$

针孔相机

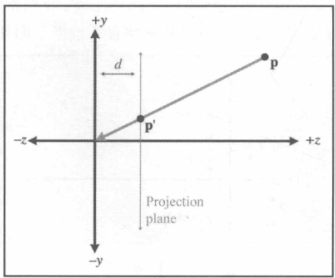
投影到 z = -d 平面

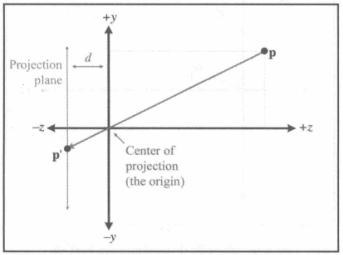
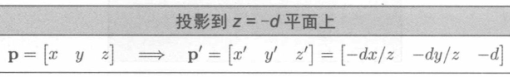
投影到 z = d 平面

投影透视矩阵

投影透视矩阵